Image and Preimage
Via images and preimages we describe how functions work on sets.
Discover Bridges
Study Image and Preimage
For every well-defined map \(f: X\to Y\) and \(A\subset X\), \(B \subset Y\) we are interested in the following sets:
Definition 1. Let \(f: X\rightarrow Y\) be a function and \(A\subset X\) and \(B\subset Y\) some sets.
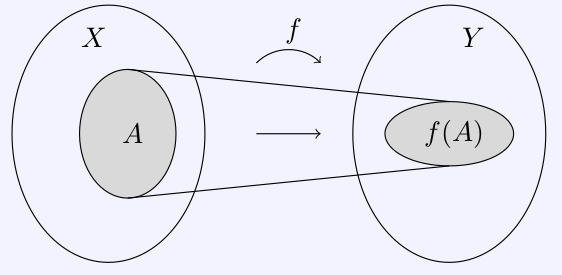
\[f(A):= \{ f(x): x\in A\}\] is called the image of \(A\) under \(f\).
\[f^{-1}(B):= \{ x\in X: f(x) \in B
\}\] is called the preimage of \(B\) under \(f\).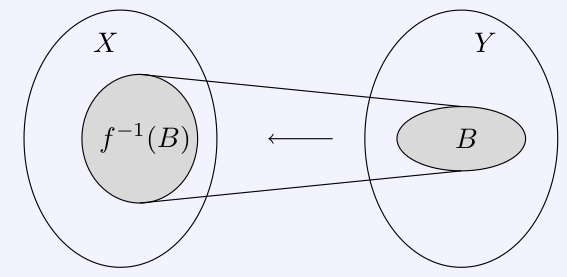 
Note that the preimage can also be the empty set if none of the elements in \(B\) are “hit” by the map.
To describe the behaviour of a map, the following sets are very important:
Definition 2 (Range and fiber). Let \(f: X\rightarrow Y\) be a map. Then \[\begin{aligned} \mathrm{Ran}(f) &:= f(X) = \{ f(x) : x \in X \} \end{aligned}\] is called the range of \(f\). For each \(y\in Y\) the set \[\begin{aligned} f^{-1}(\{y \}) &:= \{ x \in X : f(x) = y \} \end{aligned}\] is called a fiber of \(f\).
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.