Application of Taylor's Theorem
Calculate an approximation via Taylor's Theorem
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Taylor's Theorem | An approximation method for differentiable functions. |
Show consequences
| Concept | Content |
|---|---|
| Proof of Taylor's Theorem | Derive an approximation result from the generalised mean value theorem. |
Study Application of Taylor’s Theorem #
The application of Taylor’s formula is twofold: First, it gives a polynomial that approximates a given function quite fine in some neighbourhood. The second application is the computation of values of “complicated functions”. We will present examples for both kinds of application.
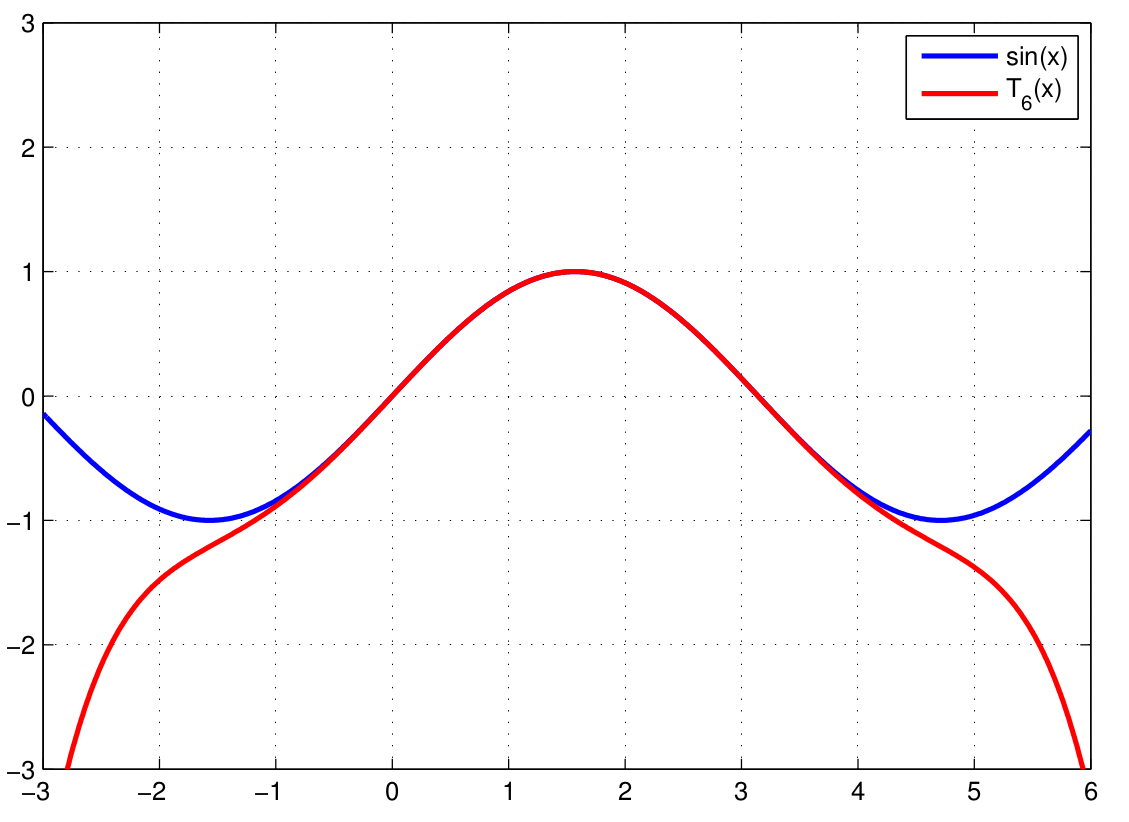
Example 1. Consider the function \(f(x)=\sin(x)\). We want to determine the Taylor polynomial of degree 6 with expansion point \(x_0=\frac\pi2\). Since we have \[\sin'(x)=\cos(x),\quad\sin''(x)=-\sin(x),\quad\sin^{(3)}(x)=-\cos(x),\] \[\sin^{(4)}(x)=\sin(x),\quad\sin^{(5)}(x)=\cos(x),\quad\sin^{(6)}(x)=-\sin(x)\] and \[\sin(x_0)=\sin\left(\frac\pi2\right)=1,\quad \cos(x_0)=\cos\left(\frac\pi2\right)=0,\] the Taylor polynomial of degree 6 is given by \[T_6(x)=1-\frac12\left(x-\frac{\pi}{2}\right)^2+\frac{1}{24}\left(x-\frac{\pi}{2}\right)^4-\frac1{720}\left(x-\frac{\pi}{2}\right)^6.\] The remainder term reads \[R_6(x,x_0)=\frac{\sin^{(7)}(\hat{x})}{7!}\left(x-\frac{\pi}{2}\right)^{7} =\frac{-\cos(\hat{x})}{5040}\left(x-\frac{\pi}{2}\right)^{7}.\] Taking into account that \(|\cos(x)|\leq1\) for all \(x\in\mathbb{R}\), we have that \[|R_6(x,x_0)|\leq\frac{\left|x-\frac{\pi}{2}\right|^{7}}{5040}.\] This leads to the estimate \[|\sin(x)-T_6(x)|=|R_6(x,x_0)|\leq\frac{\left|x-\frac{\pi}{2}\right|^{7}}{5040}.\]
Example 2. We want to compute \(\log(1.2)\) up to 3 digit precision. A nice expansion point is \(x_0=1\) since we know the precise values of \(\log^{(k)}(1)\). Consider \[\log'(x)=\frac1x,\quad \log''(x)=-\frac{1!}{x^2},\] \[\log^{(3)}(x)=\frac{2!}{x^3},\quad\log^{(4)}(x)=-\frac{3!}{x^4}\] and therefore, the Taylor polynomial of degree 3 is given by \[T_3(x)=(x-1)-\frac12(x-1)^2+\frac13(x-1)^3.\] In particular, we have \[T_3(1.2)=0.2-\frac12\cdot 0.2^2+\frac13 \cdot 0.2^3=\frac{137}{750}.\] Now we estimate \(|\log(1.2)-\frac{137}{750}|\): The remainder term is given by \[R_3(x,x_0)=-\frac{3!}{\hat{x}^4}\frac{(x-x_0)^{4}}{4!}=-\frac{(x-x_0)^{4}}{4\hat{x}^4}\] for some \(\hat{x}\) between \(x\) and \(x_0\). For \(x=1.2\), \(x_0=1\) we have \(1<\hat{x}<1.2\) and therefore \[| R_3(1.2,1) | =\frac{(0.2)^{4}}{4\hat{x}^4}=4\cdot10^{-4}\frac{1}{\hat{x}^4}\leq4\cdot10^{-4}.\] This leads to \[|\log(1.2)-0.182\overline{6}|=|R_3(1.2,1)|\leq4\cdot10^{-4},\] so we have determined \(\log(1.2)\) up to three digits.
Theorem 3. Let \(I\subset \mathbb{R}\) be an open interval, \(n\in\mathbb{N}\) and \(f:I\rightarrow\mathbb{R}\) an \(n\)-times continuously differentiable function. Suppose that for \(a\in I\) holds \[f'(a)=f''(a)=\dots=f^{(n-1)}(a)=0\quad \text{and}\quad f^{(n)}(a)\neq 0 \ .\] If \(n\) is odd, then \(a\) is not a local extremum. If \(n\) is even and \(f^{(n)}(a)> 0\), then \(a\) is a local minimum. If \(n\) is even and \(f^{(n)}(a)< 0\), then \(a\) is a local maximum.
Proof: By assumption the Taylor expansion of \(f\) of degree \(n-1\) in the expansion point \(a\) reads: \[\label{eq:locext1} f(x)=f(a)+\frac{f^{n}(z)}{n!}(x-a)^n\] where \(z=z(x)\) lies between \(x\) and \(a\). Since \(f^{(n)}\) is continuous and \(f^{(n)}(a)\neq 0\), there is a neighbourhood \(U:=~(a-\varepsilon,a+\varepsilon)~\subset I\), \(\varepsilon>0\), of \(a\) such that \(f^{(n)}(x)\neq 0\) for all \(x\in U\). This means that for all \(x\in U\), \(f^{(n)}(x)\) and \(f^{(n)}(a)\) have the same sign. Then for any \(x_l \in~(a-\varepsilon,a)\) and any \(x_r \in~(a,a+\varepsilon)\) Theorem 3 implies that for \(z_l:=z(x_l)\in~(x_l,a)\) and \(z_r:=z(x_r)\in~(a,x_r)\) holds \[f(x_l) = f(a)+\frac{f^{n}(z_l)}{n!}(x_l-a)^n ,\] \[f(x_r) = f(a)+\frac{f^{n}(z_r)}{n!}(x_r-a)^n\] and \(0\neq f^{n}(a), f^{n}(z_l),f^{n}(z_r)\) have the same sign. If \(n\) is odd, then \((x_l-a)^n < 0 < (x_r-a)^n\) and therefore either \(f(x_l)<f(a)<f(x_r)\) or \(f(x_l)>f(a)>f(x_r)\) so that \(a\) is not a local extremum. If \(n\) is even and \(f^{(n)}(a)>0\), then \((x_l-a)^n,(x_r-a)^n >0\) and \(f(x_l),f(x_r)>f(a)\) so that \(a\) is a local minimum. Finally, if \(n\) is even and \(f^{(n)}(a)<0\), then \((x_l-a)^n,(x_r-a)^n >0\) and \(f(x_l),f(x_r)<f(a)\) so that \(a\) is a local maximum. \(\Box\)
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.
