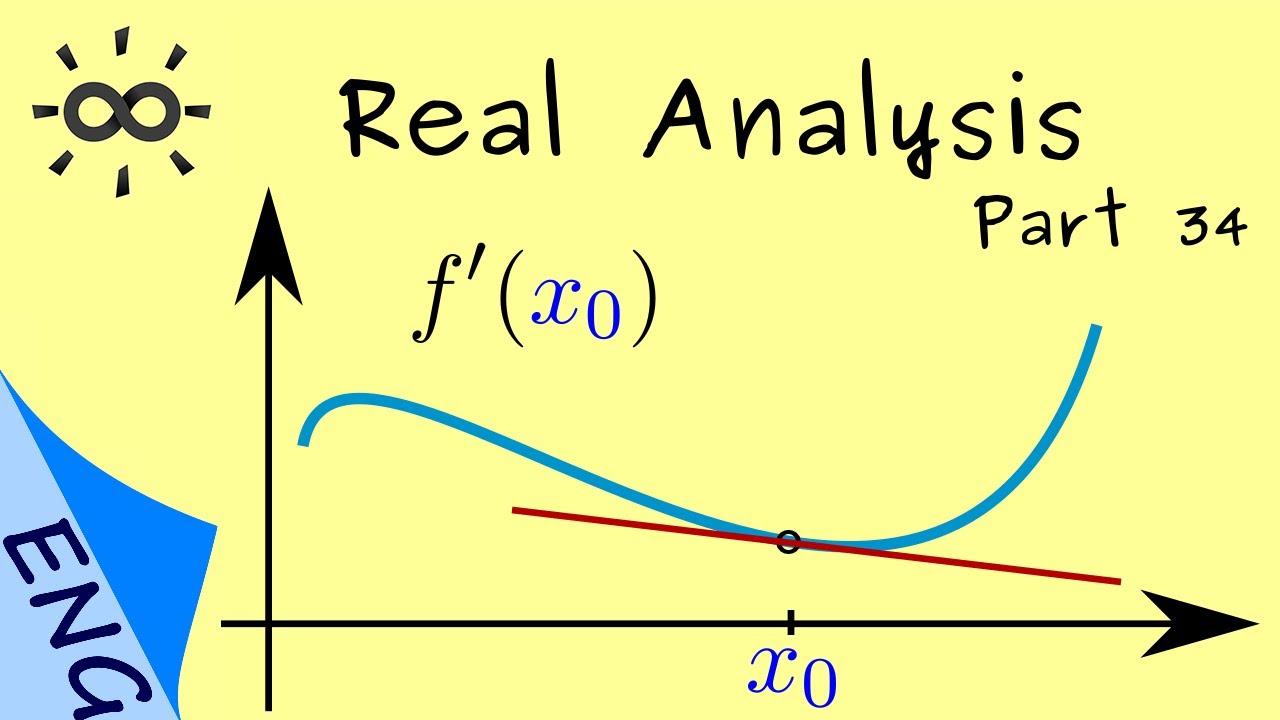
Differentiability
How to quantify the rate of change of a function.
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Continuity | The concept that relates functions with convergent sequences. |
Show consequences
| Concept | Content |
|---|---|
| Chain Rule | How to differentiate compositions of functions. |
| Higher Derivatives | Taking derivatives of derivatives of differentiable functions. |
| Examples of Differentiable Functions | Calculation of derivatives by example. |
| Sum and Product Rule | Useful rules for differentiating sums or products of differentiable functions. |
| Rolle's Theorem | The derivatives of functions with equal boundary conditions always have at least one zero. |
| Uniform Convergence for Differentiable Functions | Compatibility of differentiability with uniform limits. |
| First Fundamental Theorem of Calculus | Linking differentiation and integration. |
| Substitution Rule for Integration | An important integration rule. |
| Second Fundamental Theorem of Calculus | Characterization of all antiderivatives |
Study Differentiability #
To motivate the problem, consider the functions \(f,g:\mathbb{R}\to\mathbb{R}\) with \(f(x)=x^2\) and \(g(x)=|x|\).
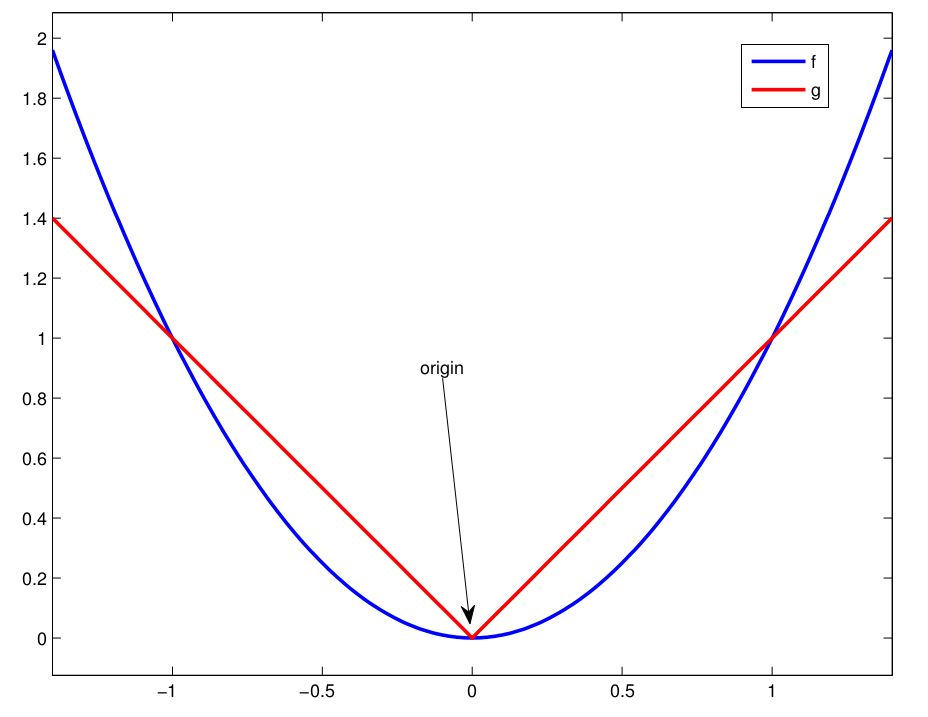
As we already know, both these functions are continuous. Let us now focus on the qualitative behavior of the functions at the origin.
| \(f\) | \(g\) |
|---|---|
| smooth | sharp bend |
| there is a unique tangent | no unique tangent |
A straight line \(y(t)\) going through the points \((x_0,f(x_0))\) and \((x,f(x))\) is called secant 1 of \(f\) through these points. It is given by \[y(t)=f(x_0)+\frac{f(x_0)-f(x)}{x_0-x}(t-x_0) .\] In particular, the slope of \(y\) is the difference quotient \[\frac{f(x_0)-f(x)}{x_0-x}=\frac{f(x)-f(x_0)}{x-x_0}.\]
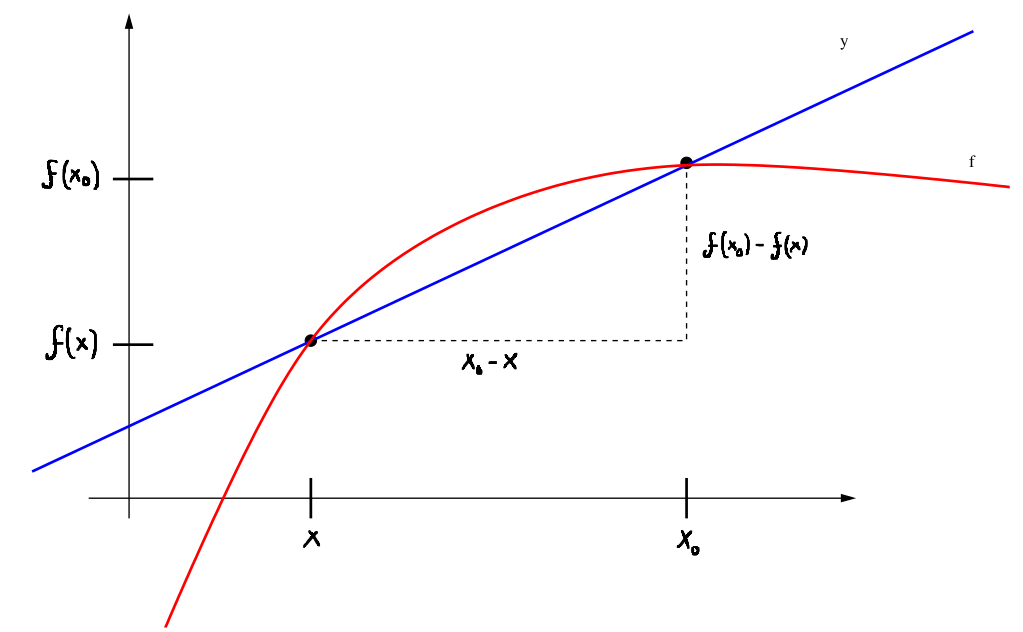
If we now let \(x\) tend to \(x_0\), we obtain a tangent of \(f\) at \(x_0\). This leads to the following definition.
Definition 1. Let \(I\subset\mathbb{R}\) be an interval with
more than one point or an open set. Let \(f:I\to\mathbb{R}\) be a function. Then
\(f\) is called differentiable at
\(x_0\in I\) if there exists
a function \(\Delta_{f,x_0}:I\to\mathbb{R}\) that is
continuous in \(x_0\) and, moreover,
for all \(x\in I\) holds \[f(x)=f(x_0)+(x-x_0)\cdot\Delta_{f,x_0}(x).\]
The number \(\Delta_{f,x_0}(x_0)\) is
called derivative of \(f\) at \(x_0\).
The function \(f\) is called
differentiable in \(I\) if it
is differentiable at all \(x_0\in
I\).
By solving the above equation for \(\Delta_{f,x_0}(x)\), we get for \(x\neq x_0\) that \[\Delta_{f,x_0}(x)=\frac{f(x)-f(x_0)}{x-x_0},\]
i.e., it is the difference quotient. Continuity of \(\Delta_{f,x_0}(x)\) at \(x_0\) is therefore equivalent to the
existence of the limit \[\lim_{x\to
x_0}\Delta_{f,x_0}(x)=\lim_{x\to
x_0}\frac{f(x)-f(x_0)}{x-x_0}=:f'(x_0).\] Also the following
notation is used in the literature for \(f'(x_0)\):
\(\frac{d}{dx}f(x_0)\), \(\frac{\partial}{\partial x}f(x_0)\), \(\frac{d f}{d x}|_{x=x_0}\), \(\frac{\partial f}{\partial x}|_{x=x_0}\),
\(\partial_xf(x_0)\).
The next result states that differentiability is a stronger property
than continuity.
Theorem 2. Let \(f:I\to\mathbb{R}\) be differentiable at \(x_0\in I\). Then \(f\) is continuous in \(x_0\).
Proof: By writing \[f(x)=f(x_0)+(x-x_0)\cdot\Delta_{f,x_0}(x),\] the continuity of \(\Delta_{f,x_0}\) at \(x_0\) implies the continuity of \(f\) at \(x_0\).\(\Box\)
As the following example shows, the opposite implication cannot be made, i.e., not every continuous function is differentiable.
Example 3. Consider the absolute value function
\(|\cdot|:\mathbb{R}\to\mathbb{R}\). We
already know that it is continuous. For the analysis of
differentiability, we distinguish between three cases: 1st
Case: \(x_0>0\).
Then we have that \(|x_0|=x_0\) and,
moreover, for \(x\) in some
neighbourhood of \(x_0\) holds \(|x|=x\). Therefore, we have \[\lim_{x\to x_0}\frac{|x|-|x_0|}{x-x_0}=\lim_{x\to
x_0}\frac{x-x_0}{x-x_0}=1.\] 2nd Case:
\(x_0<0\).
Then we have that \(|x_0|=-x_0\) and,
moreover, for \(x\) in some
neighbourhood of \(x_0\) holds \(|x|=-x\). Therefore, we have \[\lim_{x\to x_0}\frac{|x|-|x_0|}{x-x_0}=\lim_{x\to
x_0}\frac{-x+x_0}{x-x_0}=-1.\] 3rd Case:
\(x_0=0\).
Then the two sequences \((x_n)_{n\in\mathbb{N}}=(\frac1n)_{n\in\mathbb{N}}\),
\((y_n)_{n\in\mathbb{N}}=(-\frac1n)_{n\in\mathbb{N}}\)
both tend to \(x_0=0\). However, we
have \[\lim_{n\to
\infty}\frac{|x_n|-|x_0|}{x_n-x_0}=
\lim_{n\to \infty}\frac{|\frac1n|-|0|}{\frac1n-0}=1\] and \[\lim_{n\to \infty}\frac{|y_n|-|x_0|}{y_n-x_0}=
\lim_{n\to \infty}\frac{|-\frac1n|-|0|}{-\frac1n-0}=-1.\]
Therefore, the limit \[\lim_{x\to
0}\frac{|x|-|0|}{x-0}\] does not exist. Thus, \(|\cdot|\) is not differentiable at \(x_0=0\).
Note that, by a substitution \(h:=x-x_0\), the difference quotient can be reformulated as \[f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}.\]
The derivative \(a:=f'(x_0)\) of \(f\) in \(x_0\) can be interpreted in the following way: The linear mapping \(\varphi:\mathbb{R}\rightarrow\mathbb{R},\ x\mapsto ax\) fulfills \[\lim_{h\rightarrow 0}\frac{|f(x_0 + h)-(f(x_0)+\varphi(h))|}{|h|}=\lim_{h\rightarrow 0}\left|\frac{f(x_0+h)-f(x_0)}{h} - a \right| = 0.\] This means that the affine linear mapping \(t(h):=f(x_0)+\varphi(h)=f(x_0)+ah\), which actually is the tangent of \(f\) at \(x_0\), approximates \(f(x)\) linearly in a neighbourhood of \(x_0\) in a best possible way.
Now we consider some examples of differentiable functions.
Example 4.
Given is some constant \(c\in\mathbb{R}\). Consider the constant function \(f:\mathbb{R}\to\mathbb{R}\) with \(f(x)=c\) for all \(x\in \mathbb{R}\). Then for all \(x_0\in \mathbb{R}\) holds \[f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim_{x\to x_0}\frac{c-c}{x-x_0}=0.\]
Given is some constant \(c\in\mathbb{R}\). Consider the linear function \(f:\mathbb{R}\to\mathbb{R}\) with \(f(x)=cx\) for all \(x\in \mathbb{R}\). Then for all \(x_0\in \mathbb{R}\) holds \[f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=\lim_{x\to x_0}\frac{cx-cx_0}{x-x_0}=\lim_{x\to x_0}c\frac{x-x_0}{x-x_0}=c.\]
For determining the derivatives of \(\exp\), \(\sinh\), \(\cosh\), \(\sin\) and \(\cos\), we first determine the following limit for \(\lambda\in\mathbb{C}\): \[\lim_{h\to0}\frac{\exp(\lambda h)-1}{h}.\] By Theorem [thm:expest], we know that for \(h\in\mathbb{R}\) with \(|\lambda h|<2\) \[\exp(\lambda h)=1+\lambda h+r_2(\lambda h)\] with \(|r_2(\lambda h)|\leq |\lambda h|^2\). Therefore, \[\lim_{h\to0}\frac{\exp(\lambda h)-1}{h}=\lim_{h\to0}\frac{1+\lambda h+r_2(\lambda h)-1}{h}=\lim_{h\to0}\left(\lambda+\frac{r_2(\lambda h)}{h}\right) =\lambda.\] We can further conclude \[\lim_{h\to0}\frac{\exp(\lambda(x_0+h))-\exp(\lambda x_0)}{h}= \exp(\lambda x_0)\cdot\lim_{h\to0}\frac{\exp(\lambda h)-1}{h}=\lambda \exp(\lambda x_0).\] This has manifold consequences for the derivatives of exponential, hyperbolic and trigonometric functions: \[\exp'(x_0)=\lim_{h\to0}\frac{\exp(x_0+h)-\exp(x_0)}{h}=\exp(x_0),\] i.e., \(\exp'=\exp\).
We can further conclude that \[\begin{aligned} \sinh'(x_0)=&\lim_{h\to0}\frac{\sinh(x_0+h)-\sinh(x_0)}{h}\\=& \frac12\lim_{h\to0}\left(\frac{\exp(x_0+h)-\exp(x_0)}{h}+\frac{-\exp(-(x_0+h))+\exp(-x_0)}{h}\right)\\ =&\frac12(\exp(x_0)+\exp(-x_0))=\cosh(x_0). \end{aligned}\] Analogously, we can show that \(\cosh'=\sinh\). Now consider the trigonometric functions: \[\begin{aligned} \sin'(x_0)=&\lim_{h\to0}\frac{\sin(x_0+h)-\sin(x_0)}{h}\\ =&\frac1{2i}\lim_{h\to0}\left(\frac{\exp(i(x_0+h))-\exp(ix_0)}{h}+\frac{-\exp(-i(x_0+h))+\exp(-ix_0)}{h}\right)\\ =&\frac1{2i}(i\exp(ix_0)+i\exp(-ix_0))=\cos(x_0) \end{aligned}\] and \[\begin{aligned} \cos'(x_0)=&\lim_{h\to0}\frac{\cos(x_0+h)-\cos(x_0)}{h}\\ =&\frac1{2}\lim_{h\to0}\left(\frac{\exp(i(x_0+h))-\exp(ix_0)}{h}+\frac{\exp(-i(x_0+h))-\exp(-ix_0)}{h}\right)\\ =&\frac1{2}(i\exp(ix_0)-i\exp(-ix_0))\\=& -\frac1{2i}(\exp(ix_0)-\exp(-ix_0))=-\sin(x_0). \end{aligned}\]
from the Latin word secare = “to cut”↩︎
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.