Operations on Sets
Sets can be joined or intersected in order to create new sets.
Discover Bridges
Study Operations on Sets
We remember the important operations for sets:
\(M_1 \cup M_2 := \{ x \mid x\in M_1 \vee x \in M_2 \}\) (union)
\(M_1 \cap M_2 := \{ x \mid x \in M_1 \wedge x \in M_2\}\) (intersection)
\(M_1 \setminus M_2 := \{ x \mid x \in M_1 \wedge x \not\in M_2 \}\) (set difference)
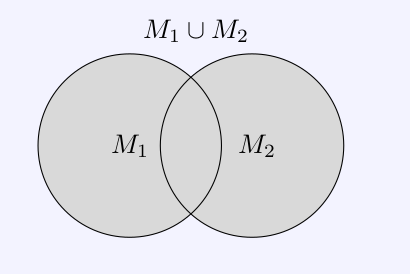
Definition 1 (Set compositions). The union \(M_1\cup M_2\) is the new set that consists exactly of the objects that are elements of \(M_1\) or \(M_2\).
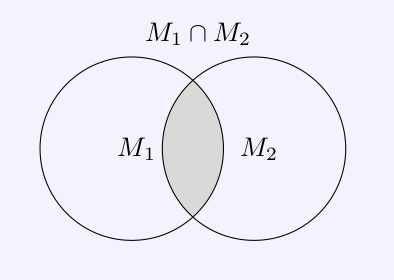
The intersection \(M_1\cap M_2\) is the new set whose elements are the objects that are elements of \(M_1\) and \(M_2\).
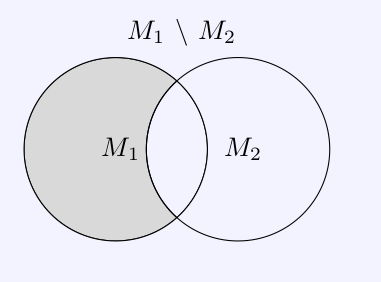
We write \(M_1\setminus M_2\) for the set difference whose elements are the objects that are elements of \(M_1\) but not elements of \(M_2\).
A subset of \(M_2\) is each set whose elements are also elements of \(M_2\).
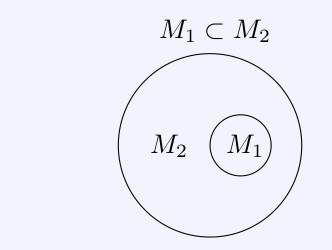
Definition 2 (Complement set). Let \(X\) be a set. Then for a subset \(M \subset X\) there is a unique complement of \(M\) with respect to \(X\): \[M^c := X \setminus M = \{ x \in X \mid x \notin M \}\]
Definition 3 (Product set, Cartesian product). The Cartesian product of two sets \(A,B\) is given as the set of all pairs (two elements with order): \[A \times B := \{ (a,b) \mid a \in A, b \in B\}\] In the same sense, for sets \(A_1, \ldots, A_n\) the set of all \(n\)-tupels is defined: \[A_1 \times \cdots \times A_n := \{ (a_1,\ldots, a_n) \mid a_1 \in A_1, \ldots, a_n \in A_n\}\]
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.