Uniform Limits of Continuous Functions
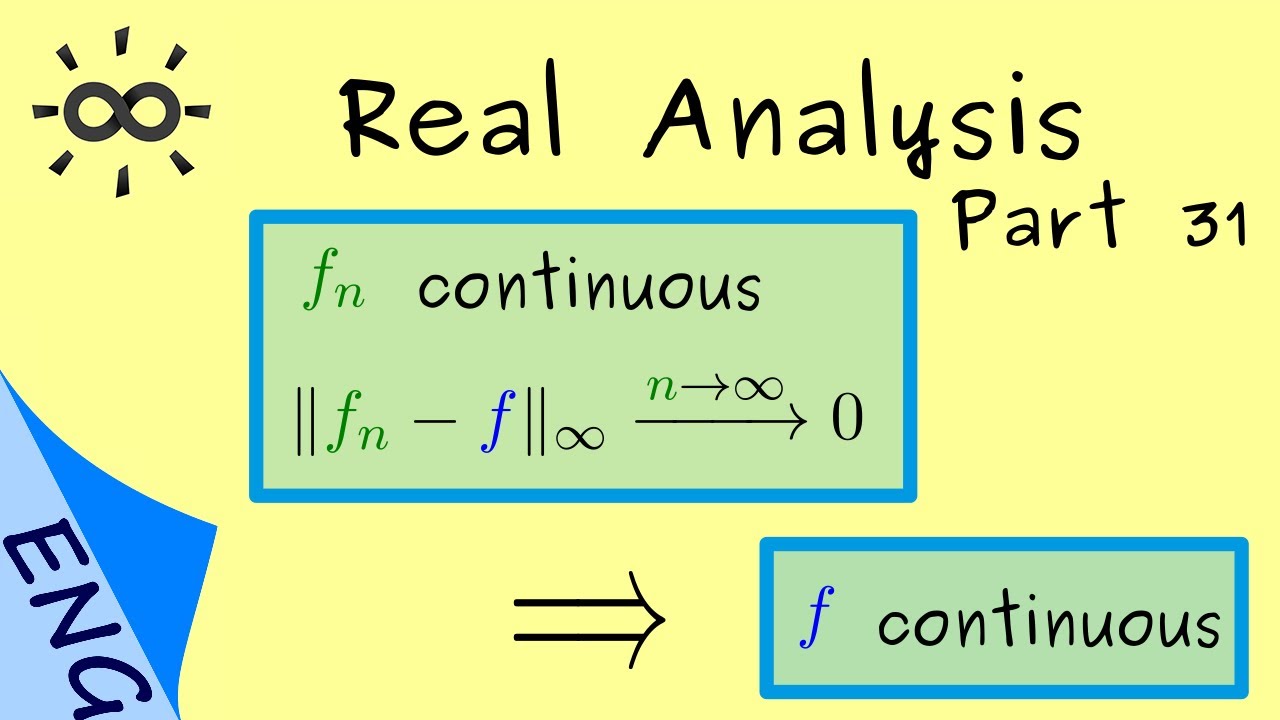
How to preserve continuity in the limit of a sequence of continuous functions.
Discover Bridges
Study Uniform Limits of Continuous Functions
Now we show that a uniformly convergent sequence of continuous functions has to converge to a continuous function.
Theorem 1. Let \(I\subset \mathbb{K}\) and let \((f_n)_{n\in\mathbb{N}}\) be a sequence of continuous functions \(f_n:I\to\mathbb{K}\) that uniformly converges to some \(f:I\to\mathbb{K}\). Then \(f\) is continuous.
Proof: Let \(\varepsilon>0\) and let \(x_0\in I\). Since \((f_n)_{n\in\mathbb{N}}\) converges uniformly to \(f:I\to\mathbb{K}\), there exists some \(N\) such that for all \(n\geq N\) and \(x\in I\) holds \[|f(x)-f_n(x)|<\frac\varepsilon3.\] Since \(f_n\) is continuous on \(I\), there exists some \(\delta>0\) such that for all \(x\in I\) with \(|x-x_0|<\delta\) holds \[|f_n(x_0)-f_n(x)|<\frac\varepsilon3.\] Altogether, we then have \[\begin{aligned} |f(x)-f(x_0)|=&\,|f(x)-f_n(x)+f_n(x)-f_n(x_0)+f_n(x_0)-f(x_0)|\\ \leq &\,|f(x)-f_n(x)|+|f_n(x)-f_n(x_0)|+|f_n(x_0)-f(x_0)|\\ < &\,\frac\varepsilon3+\frac\varepsilon3+\frac\varepsilon3=\varepsilon. \end{aligned}\] Therefore, \(f\) is continuous by the \(\varepsilon\)-\(\delta\) criterion. \(\Box\)
Remark 2. The above result also gives a sufficient characterisation for a sequence of pointwisely convergent functions \((f_n)_{n\in\mathbb{N}}\) that are not uniformly convergent: If \((f_n)_{n\in\mathbb{N}}\) converges to a discontinuous function, then this sequence cannot be uniformly convergent. For instance, consider the sequence \((f_n)_{n\in\mathbb{N}}\) with \(f_n:[0,1]\to\mathbb{R}\), \(x\mapsto x^n\). The pointwise limit is given by \[f(x)=\lim_{n\to\infty}f_n(x)=\begin{cases}0&,\text{ if }x\in[0,1),\\1&,\text{ if }x=1,\end{cases}\] which is discontinuous at \(x=1\) though each \(f_n\) is continuous. Therefore, this sequence cannot be uniformly convergent.
Discuss your questions by typing below.
Solve the Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.