Exponential Function
A special function that can be defined via a power series.
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Injectivity, Surjectivity, Bijectivity | These are important notions for maps. |
| Absolute Convergence | A strong concept of convergence of series. |
| Cauchy Product | A special way to multiply two absolutely convergent sequences. |
| Quotient Criterion | An important criterion to prove absolute convergence by means of ratios of the underlying sequence's terms. |
| Sequences of Bounded Functions | The concept of sequences but for functions instead of real numbers. |
| Series and Partial Sums | A series is a sequence of partial sums. |
| Continuity | The concept that relates functions with convergent sequences. |
Show consequences
| Concept | Content |
|---|---|
| Logarithm Function | The inverse of the exponential function. |
| Examples of Differentiable Functions | Calculation of derivatives by example. |
| Substitution Rule for Integration | An important integration rule. |
Study Exponential Function #
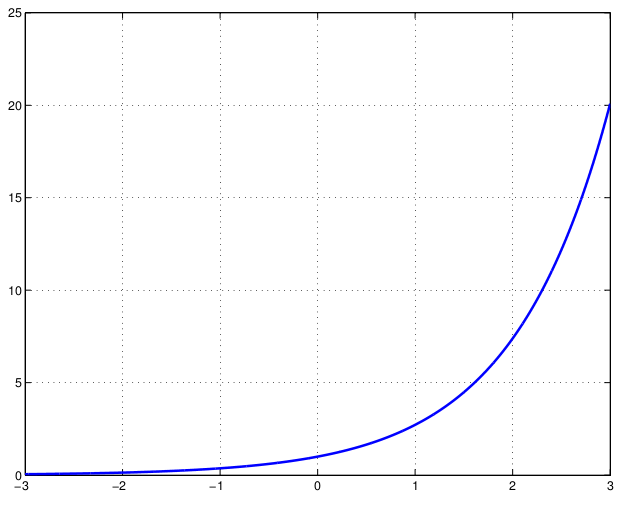
Definition 1. The exponential function \(\exp:\mathbb{K}\to\mathbb{K}\) is defined as \[\exp(x)=\sum_{k=0}^\infty\frac{x^k}{k!}.\] The number \[e=\exp(1)=\sum_{k=0}^\infty\frac{1}{k!}\] is called Euler’s number.
For Euler’s number holds \[e\approx 2.718281828459046.\] We already saw as an example application of the quotient criterion that the above defined series converges for all \(x\in\mathbb{K}\). Now we present an estimate for \(\exp(x)\) if the series is replaced by a finite sum.
Theorem 2. For \(n\in\mathbb{N}\) and \(x\in\mathbb{K}\) with \(|x|\leq1+\frac{n}2\) holds \[\exp(x)=\sum_{k=0}^n\frac{x^k}{k!}+r_n(x)\qquad\text{with }|r_n(x)|\leq2\frac{|x|^{n+1}}{(n+1)!}.\]
Theorem 3. Properties of the Exponential Function
For all \(x,y\in\mathbb{C}\) holds \(\exp(x+y)=\exp(x)\exp(y)\).
For all \(x\in\mathbb{C}\) holds \(\exp(\overline{x})=\overline{\exp(x)}\) (\(\overline{y}\) denotes the complex conjugate of \(y\in\mathbb{C}\)).
For all \(x\in\mathbb{C}\) holds \(\exp(x)\neq0\) and \[\exp(-x)=\frac1{\exp(x)}.\]
For \(x\in\mathbb{R}\) with \(x\geq0\) holds \(\exp(x)\geq1\). Where \(\exp(x)=1 \Leftrightarrow x=0\).
For \(x\in\mathbb{R}\) with \(x<0\) holds \(0<\exp(x)<1\).
\(\exp\) in continuous.
\(\exp:\mathbb{R}\to\mathbb{R}\) is strictly monotonically increasing.
\(\lim_{x\to\infty}\exp(x)=\infty\) and \(\lim_{x\to-\infty}\exp(x)=0\).
\(\exp:\mathbb{R}\to(0,\infty)\) is bijective.
For all \(x\in\mathbb{C}\) holds \(|\exp(x)|=\exp(\Re(x))\).
Proof:
Already shown as an example application of the cauchy product of series.
Since we have \(\overline{x_1+x_2}=\overline{x_1}+\overline{x_2}\) and \(\overline{x_1x_2}=\overline{x_1} \cdot \overline{x_2}\) for all \(x_1,x_2\in\mathbb{C}\), we have \[\exp(\bar{x})=\sum_{k=0}^\infty\frac{\bar{x}^k}{k!}=\overline{\sum_{k=0}^\infty\frac{{x}^k}{k!}}=\overline{\exp(x)}.\]
By definition of \(\exp\), we have \(\exp(0)=1\). From (i), we get \(\exp(x)\cdot\exp(-x)=\exp(x-x)=\exp(0)=1\). Then the statement follows.
From \(x\geq0\), we get \[\exp(x)=\sum_{k=0}^\infty\frac{x^k}{k!}=1+\sum_{k=1}^\infty\frac{x^k}{k!}\geq1.\] It is immediately clear that equality only holds for \(x=0\).
If \(x<0\), we get from (iii) that \(\exp(-x)>1\). Then, \(\exp(x)=\frac1{\exp(-x)}<1\).
First we show that \(\exp\) is continuous at \(0\).
Let \(x_1,x_2\in\mathbb{R}\) with \(x_1> x_2\). Then we have \(x_1-x_2>0\) and thus, by (iv), \(\exp(x_1-x_2)>1\). Since \(\exp(x_2)>0\), we have \[\exp(x_1)=\exp(x_2)\exp(x_1-x_2)>\exp(x_2).\]
The fact \(\lim_{x\to\infty}\exp(x)=\infty\) follows, since we have for \(x>0\) that \[\exp(x)=\sum_{k=0}^\infty\frac{x^k}{k!}=1+x+\sum_{k=2}^\infty\frac{x^k}{k!}>1+x.\] The statement (iii) then directly implies \(\lim_{x\to-\infty}\exp(x)=0\).
The injectivity of \(\exp:\mathbb{R}\to(0,\infty)\) follows from (vii). It remains to show surjectivity. Let \(y\in(0,\infty)\).
Since \(\lim_{x\to-\infty}\exp(x)=0\), there exists some \(x_0\in\mathbb{R}\) such that \(\exp(x_0)<y\).
Since \(\lim_{x\to\infty}\exp(x)=\infty\), there exists some \(x_1\in\mathbb{R}\) such that \(\exp(x_1)>y\).
Now, by the Mean Value Theorem, (remember that \(\exp\) is continuous), there exists some \(x\in\mathbb{R}\) with \(\exp(x)=y\).Let \(x=x_1+ix_2\) with \(x_1=\Re(x)\), \(x_2=\Im(x)\). Then \[| \exp(x) | = |\exp(x_1+ix_2)|=|\exp(x_1)\exp(ix_2)|=|\exp(x_1)||\exp(ix_2)|.\] If we now show that \(|\exp(ix_2)|=1\), the result is proven: Making use of (ii), we obtain \[|\exp(ix_2)|^2=\exp(ix_2)\cdot\overline{\exp(ix_2)}=\exp(ix_2-ix_2)=\exp(0)=1.\]\(\Box\)
Fabian Gabel and Marcus Waurick. Well-defined & Wonderful podcast, marcus-waurick.de.
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.