Epsilon-Delta Definition
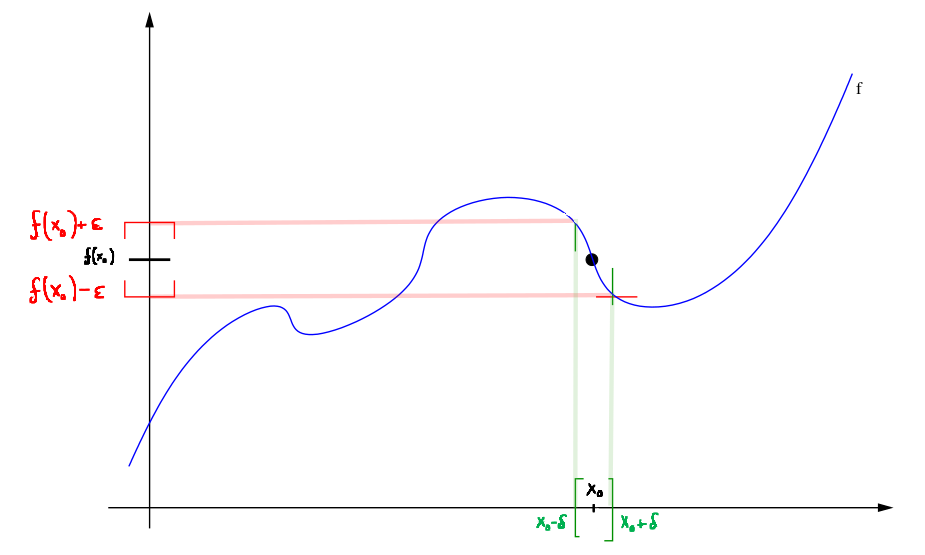
A different notion of continuity using open intervals. If the input to a continuous function varies less than delta, then the output values should vary less than epsilon.
Discover Bridges
Study Epsilon-Delta Definition
Theorem 1 (\(\varepsilon\)-\(\delta\) criterion for continuity). Let \(I\subset \mathbb{K}\) and \(f:I\to\mathbb{K}\) be a function. Let \(x_0\in I\). Then the following two statements are equivalent.
\(f\) is continuous in \(x_0\);
For all \(\varepsilon>0\) there exists some \(\delta>0\) such that for all \(x\in I\) with \(|x-x_0|<\delta\) holds \[|f(x)-f(x_0)|<\varepsilon.\]
Proof:
“(i)\(\Rightarrow\)(ii)”: Assume that
(ii) is not fulfilled, i.e., there exists some \(\varepsilon>0\), such that for all \(\delta>0\), there exists some \(x\in I\setminus\{x_{0}\}\) with \(|x-x_0|<\delta\) and \(|f(x)-f(x_0)|>\varepsilon\). As
a consequence, for all \(n\in\mathbb{N}\), there exists some \(x_n\in I\setminus\{x_{0}\}\) with \[|x_0-x_n|<\frac1n\;\text{ and
}\;|f(x_n)-f(x_0)|>\varepsilon.\] Therefore, the sequence
\((x_n)_{n\in\mathbb{N}}\) converges to
\(x_0\), but \(|f(x_n)-f(x_0)|>\varepsilon\), i.e.,
\(f(x_n)\) is not converging to \(f(x_0)\).
“(ii)\(\Rightarrow\)(i)”: Let \((x_n)_{n\in\mathbb{N}}\) be a sequence in
\(I\backslash\{x_0\}\) that converges
to \(x_0\). Let \(\varepsilon>0\). Then there exists some
\(\delta>0\) such that for all \(x\in I\) with \(|x-x_0|<\delta\) holds \(|f(x)-f(x_0)|<\varepsilon\). Since \((x_n)_{n\in\mathbb{N}}\) converges to \(x_0\), there exists some \(N\) such that for all \(n\geq N\) holds \(|x_n-x_0|<\delta\). By the \(\varepsilon\)-\(\delta\)-criterion, we have then for all
\(n\geq N\) that \[|f(x_n)-f(x_0)|<\varepsilon.\] Hence,
\((f(x_n))_{n\in\mathbb{N}}\) converges
to \(f(x_0)\).\(\Box\)
Fabian Gabel and Marcus Waurick. Well-defined & Wonderful podcast, marcus-waurick.de.
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.