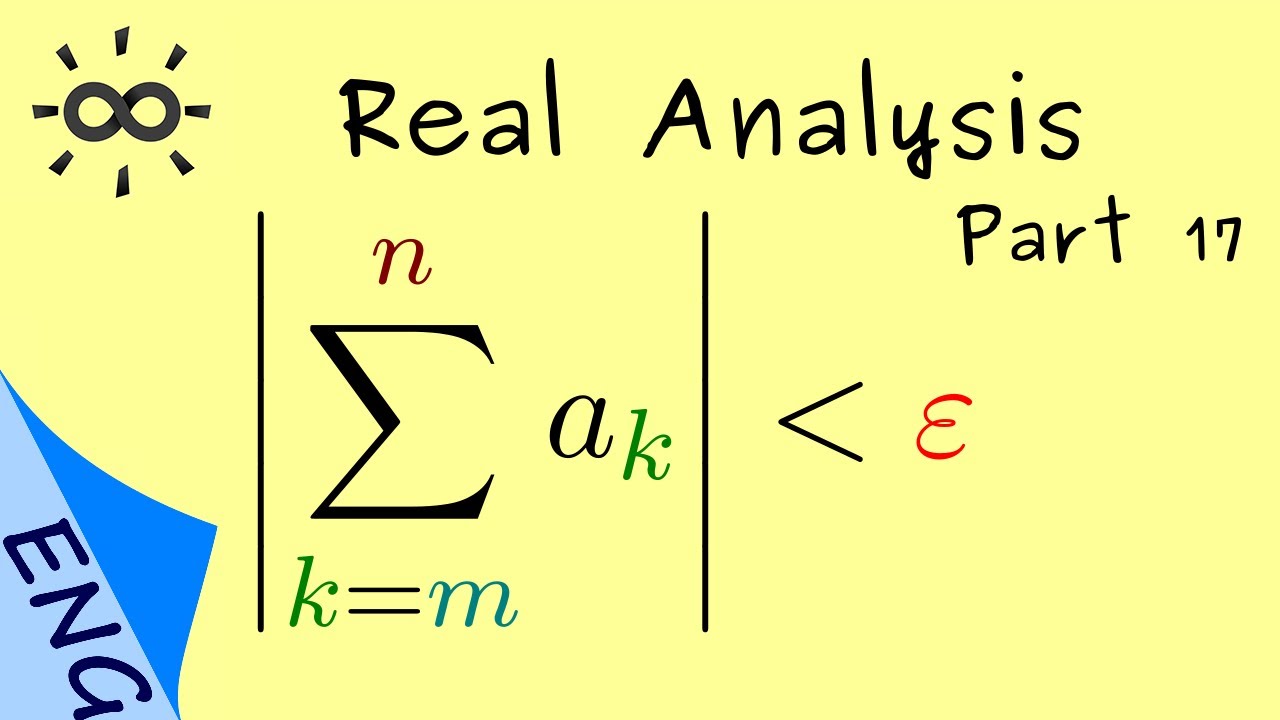Cauchy Criterion
A series converges if its partial sums form a Cauchy sequence. As a consequence, for a convergent series, the underlying sequence necessarily needs to converge to zero.
Discover Bridges
Study Cauchy Criterion
Theorem 1 (Cauchy Criterion). A series \(\displaystyle\sum_{k=1}^\infty a_k\) in \(\mathbb{R}\) is convergent if and only if for all \(\varepsilon>0\), there exists some \(N\) such that for all \(n\geq m\geq N\) holds \[\left|\sum_{k=m}^n a_k\right|<\varepsilon.\]
Proof: By the theorems on completeness and
convergence of cauchy sequences, a series converges if and only if the
sequence \((s_{n})_{n\in\mathbb{N}}\)
of partial sums is a Cauchy sequence.
On the other hand, for \(n\geq m\), we
have \[\left|s_n-s_{m-1}\right|=\left|\sum_{k=m}^n
a_k\right|.\] Therefore, the Cauchy criterion is really
equivalent to the fact that \((s_{n})_{n\in\mathbb{N}}\) is a Cauchy
sequence in \(\mathbb{R}\).\(\Box\)
As a corollary, we can formulate the following criterion.
Theorem 2 (Necessary criterion for convergence of series). Let \[\sum_{k=1}^\infty a_k\] be a convergent series in \(\mathbb{R}\). Then \((a_n)_{n \in \mathbb{N}}\) is convergent with \[\lim_{n\to\infty}a_n=0.\]
Proof: Since the series converges, the Cauchy criterion implies that for all \(\varepsilon>0\), there exists some \(N\) such that for all \(n\geq m\geq N\) holds \[\left|\sum_{k=m}^n a_k\right|<\varepsilon.\] Now considering the special case \(n=m\), we have that for all \(n\geq N\) holds \[|a_n|<\varepsilon.\] However, this is nothing but convergence of \((a_n)_{n\in\mathbb{N}}\) to zero. \(\Box\)
Remark 3. The zero convergence of \((a_n)_{n\in\mathbb{N}}\) is by far not sufficient for convergence. We have already seen that the harmonic series diverges though the sequence \((a_n)_{n\in\mathbb{N}}=(\frac1n)_{n\in\mathbb{N}}\) converges to zero.
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.