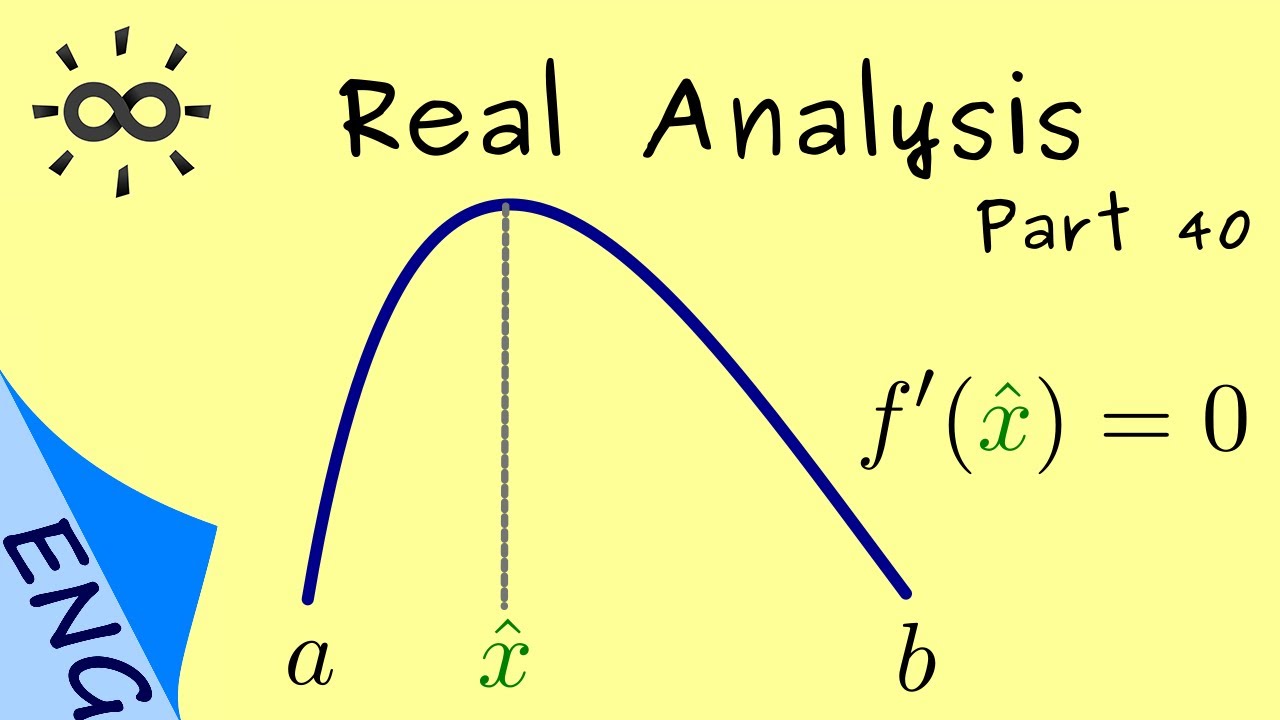
The derivatives of functions with equal boundary conditions always have at least one zero.
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
Show consequences
| Concept |
Content |
| Mean Value Theorem |
This theorem helps us to link monotonicity of a function with values of its derivative. |
Theorem 1. Let \(I\) be an interval and \(f:I \to\mathbb{R}\) be a function that is
differentiable in \(x_0\in I\). Assume
that \(x_0\) is an interior point of
\(I\) and that \(x_0\) is a local extremum. Then \(f'(x_0)=0\).
Proof: We assume that \(x_0\) is a local maximum (the case of
minimum is shown analogously). Let \(U\) be a neighbourhood of \(x_0\) with \(U\subset I\) and \(f(x_0)=\max\{f(x):\;x\in U\}\). Let \[f(x)=f(x_0)+(x-x_0)\cdot\Delta_{f,x_0}(x).\]
Assume that \(f'(x_0)=\Delta_{f,x_0}(x_0)>0\).
Since \(\Delta_{f,x_0}\) is continuous
in \(x_0\), then there exists
a neighbourhood \(V\subset U\) of \(x_0\) such that \(\Delta_{f,x_0}(x)>0\) for all \(x\in V\). Then for all \(x_1\in V\) with \(x_1>x_0\) holds \(f(x_1)=f(x_0)+(x_1-x_0)\cdot\Delta_{f,x_0}(x_1)>f(x_0)\).
This is a contradiction.
On the other hand, assume that \(f'(x_0)=\Delta_{f,x_0}(x_0)<0\).
Since \(\Delta_{f,x_0}\) is continuous
in \(x_0\), then there exists
a neighbourhood \(V\subset U\) such
that \(\Delta_{f,x_0}(x)<0\) for all
\(x\in V\). Then for all \(x_1\in V\) with \(x_1<x_0\) holds \(f(x_1)=f(x_0)+(x_1-x_0)\cdot\Delta_{f,x_0}(x_1)>f(x_0)\).
This is also a contradiction.\(\Box\)
As a consequence, we will formulate the following result stating that
derivatives of functions with equal boundary conditions have at least
one zero.
Theorem 2 (Theorem of Rolle). Let \(f:[a,b]\to\mathbb{R}\) be differentiable in
\([a,b]\) and let \(f(a)=f(b)\). Then there exists some \(x\in(a,b)\) such that \(f'(x)=0\).
Proof: If \(f\) is constant, the statement is clear
(since then \(f'(x)=0\) for all
\(x\in(a,b)\)). If \(f\) is not constant, consider the maximum
and the minimum of \(f\) on \([a,b]\) (we know by the theorem about
compactness of images under continuout functions the that they exist).
So, let \(x_-,x_+\in[a,b]\) such that
\[f(x_+)=\max\{f(x)\;:\;x\in[a,b]\},\qquad
f(x_-)=\min\{f(x)\;:\;x\in[a,b]\}.\] Then we have that \(x_+\in(a,b)\) or \(x_-\in(a,b)\) since, otherwise, \(f(x_+)=f(x_-)\) (constant).
Then \(f'(x_-)=0\) or \(f'(x_+)=0\).\(\Box\)
As a corollary, we have that for a function \(f\) differentiable in some interval \(I\), the following holds: Between two zeros
of \(f\), there always exists some
point \(x_0\) with \(f'(x_0)=0\).
Discuss your questions by typing below.