Cauchy Product
A special way to multiply two absolutely convergent sequences.
On this page
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Series and Partial Sums | A series is a sequence of partial sums. |
| Absolute Convergence | A strong concept of convergence of series. |
Show consequences
| Concept | Content |
|---|---|
| Exponential Function | A special function that can be defined via a power series. |
Study Cauchy Product #
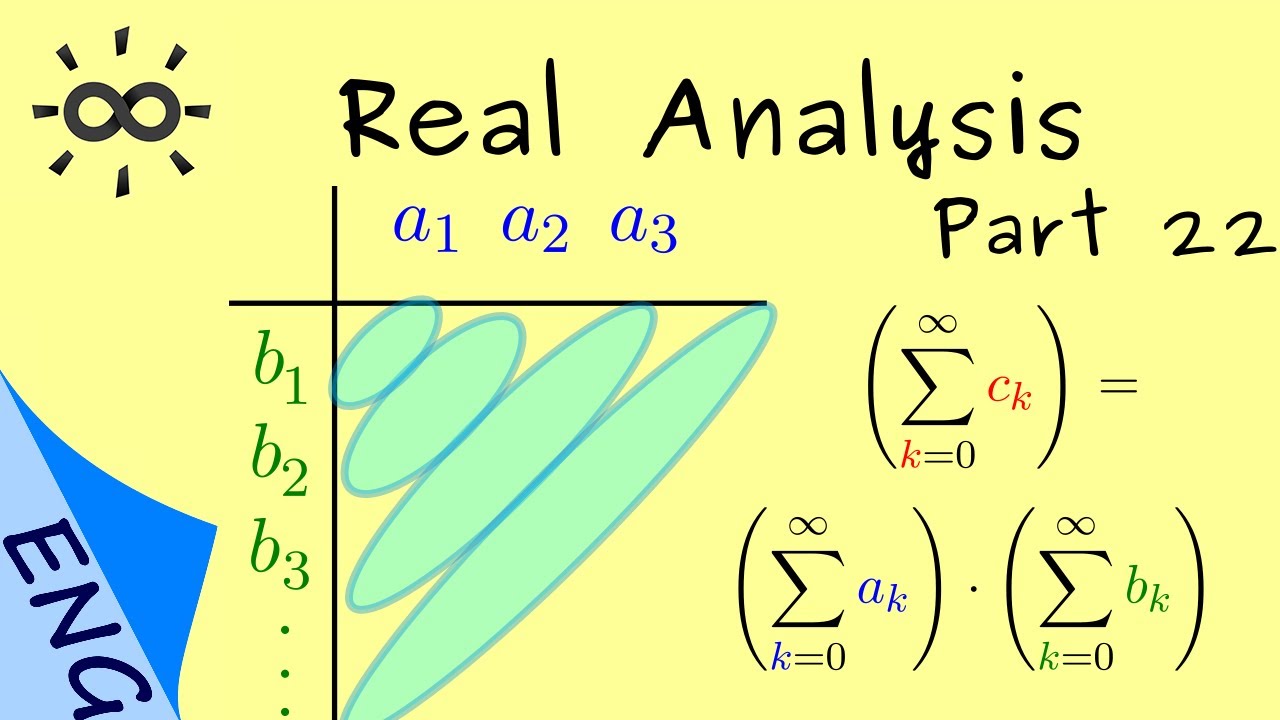
Definition 1 (Cauchy product of series). Let \(\sum_{k=0}^\infty a_k\), \(\sum_{k=0}^\infty b_k\) be two series in \(\mathbb{K}\). Then the Cauchy product of \(\sum_{k=0}^\infty a_k\), \(\sum_{k=0}^\infty b_k\) is given by \[\sum_{k=0}^\infty c_k\quad\text{ with }c_k=\sum_{l=0}^ka_lb_{k-l}.\]
Remark 2. Note that we considered series with lower summation index 0. The Cauchy product can be also defined for sequences \(\sum_{k=n_0}^\infty a_k\), \(\sum_{k=n_1}^\infty b_k\) with arbitrary \(n_0,n_1\in\mathbb{N}\) (or even \(n_0,n_1\in\mathbb{Z}\)). In this case, the Cauchy product is given by \[\sum_{k=n_0+n_1}^\infty c_k\quad\text{ with }c_k=\sum_{l=n_0}^{k-n_1}a_lb_{k-l}.\] In order to “keep the set of indices manageable”, this is not further treated here. Note that the following result about convergence properties of the Cauchy product still hold true in this above mentioned more general case.
The following theorem justifies the name “product” in the above definition.
Theorem 3 (Convergence of the Cauchy product). Let \(\sum_{k=0}^\infty a_k\), \(\sum_{k=0}^\infty b_k\) be series in \(\mathbb{K}\). Assume that \(\sum_{k=0}^\infty a_k\) is absolutely convergent and \(\sum_{k=0}^\infty b_k\) is convergent. Then the Cauchy product \(\sum_{k=0}^\infty c_k\) is absolutely convergent. Moreover, the limit satisfies \[\sum_{k=0}^\infty c_k=\left(\sum_{k=0}^\infty a_k\right)\cdot\left(\sum_{k=0}^\infty b_k\right).\]
Proof: Denote the sequence of partial sums of
\(\sum_{k=0}^\infty a_k\), \(\sum_{k=0}^\infty b_k\) and \(\sum_{k=0}^\infty c_k\) by \((A_n)_{n\in\mathbb{N}}\), \((B_n)_{n\in\mathbb{N}}\) and \((C_n)_{n\in\mathbb{N}}\), respectively.
Moreover, set \(a:=\sum_{k=0}^\infty
a_k\) and \(b=\sum_{k=0}^\infty
b_k\).
Then we have \[C_n=\sum_{k=0}^nc_k=\sum_{k=0}^n\sum_{l=0}^ka_lb_{k-l}=\sum_{k=0}^na_{n-k}\sum_{l=0}^{k}b_l=\sum_{k=0}^na_{n-k}B_k.\]
Using this expression, we obtain \[C_n=\sum_{k=0}^na_{n-k}(B_k-b)+\sum_{k=0}^na_{n-k}b=\sum_{k=0}^na_{n-k}(B_k-b)+A_nb.\]
Let \(\varepsilon>0\). Since \(\sum_{k=0}^\infty a_k\) converges
absolutely, there exists some \(N_0\)
such that for all \(n\geq N_{0}\) holds
\[|B_n-b|<\frac{\varepsilon}{4(\sum_{k=0}^{\infty}|a_k|+1)}.\]
Since \((a_{n})_{n\in\mathbb{N}}\)
converges to zero by the necessary property of sequences, there exists
some \(N_1\) such that for all \(n\geq N_{1}\) holds \[|a_{n}|<\frac{\varepsilon}{4 N_{0}\
(\sup\{|b-B_l|\,:\,l\in\mathbb{N}\}+1)}.\] Also there exists some
\(N_2\) such that for all \(n\geq N_2\) holds \[|A_{n}-a|<\frac{\varepsilon}{2(|b|+1)}.\]
Therefore, with \(N=\max\{N_0+N_1,N_2\}\), we have that for
all \(n\geq N\) holds \[\begin{aligned}
|C_n-ab|=&\;\left|\sum_{k=0}^na_{n-k}(B_k-b)+b(A_n-a)\right|
\leq \sum_{k=0}^n|a_{n-k}||B_k-b|+|b||A_n-a|\\
=&\;\sum_{k=0}^{N_{0}-1}\underbrace{|a_{n-k}|}_{\color{blue}<\frac{\varepsilon}{4N_{0}\
(\sup\{|b-B_l|\,:\,l\in\mathbb{N}\}+1)}}|B_k-b|+
\sum_{k=N_{0}}^{n}|a_{n-k}|\underbrace{|B_k-b|}_{\color{blue}<\frac{\varepsilon}{4(\sum_{k=0}^{\infty}|a_k|+1)}}+
|b|\underbrace{|A_n-a|}_{\color{blue}<\frac{\varepsilon}{2(|b|+1)}}\\
<&\;\sum_{k=0}^{N_{0}-1}\frac{\varepsilon|B_k-b|}{4N_{0}\
(\sup\{|b-B_l|\,|\,l\in\mathbb{N}\}+1)}+
\sum_{k=N_{0}}^{n}\frac{\varepsilon|a_{n-k}|}{4(\sum_{k=0}^{\infty}|a_k|+1)}+
\frac{\varepsilon|b|}{2(|b|+1)}\\
<&\;\frac{\varepsilon}{4}+\frac{\varepsilon}{4}+\frac{\varepsilon}{2}=\varepsilon
\end{aligned}\]
Example 4. Let \(x,y\in\mathbb{K}\) and consider the series \[\sum_{k=0}^\infty\frac{x^k}{k!},\qquad \sum_{k=0}^\infty\frac{y^k}{k!}\] which are absolutely convergent as shown as an Example covered in the node for the quotient criterion. Then the Cauchy product of both series is given by \(\sum_{k=0}^\infty c_k\) with \[c_k=\sum_{l=0}^k\frac{x^l}{l!}\frac{y^{k-l}}{(k-l)!}=\frac{1}{k!}\cdot\sum_{l=0}^k\begin{pmatrix}k\\l\end{pmatrix}x^ly^{k-l}.\] By the Binomial Theorem, we obtain \[\sum_{l=0}^k\begin{pmatrix}k\\l\end{pmatrix}x^ly^{k-l}=(x+y)^k.\] Hence, by the Theorem on the Cauchy product, we have \[\left(\sum_{k=0}^\infty\frac{x^k}{k!}\right)\cdot\left(\sum_{k=0}^\infty\frac{y^k}{k!}\right)=\sum_{k=0}^\infty\frac{(x+y)^k}{k!}.\] Altogether, this means that the function \[f(x)=\sum_{k=0}^\infty\frac{x^k}{k!}\] fulfills \(f(x+y)=f(x)\cdot f(y)\) for all \(x,y\in\mathbb{R}\) (and even \(x,y\in\mathbb{C}\)).
Discuss your questions by typing below.
Solve the Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.