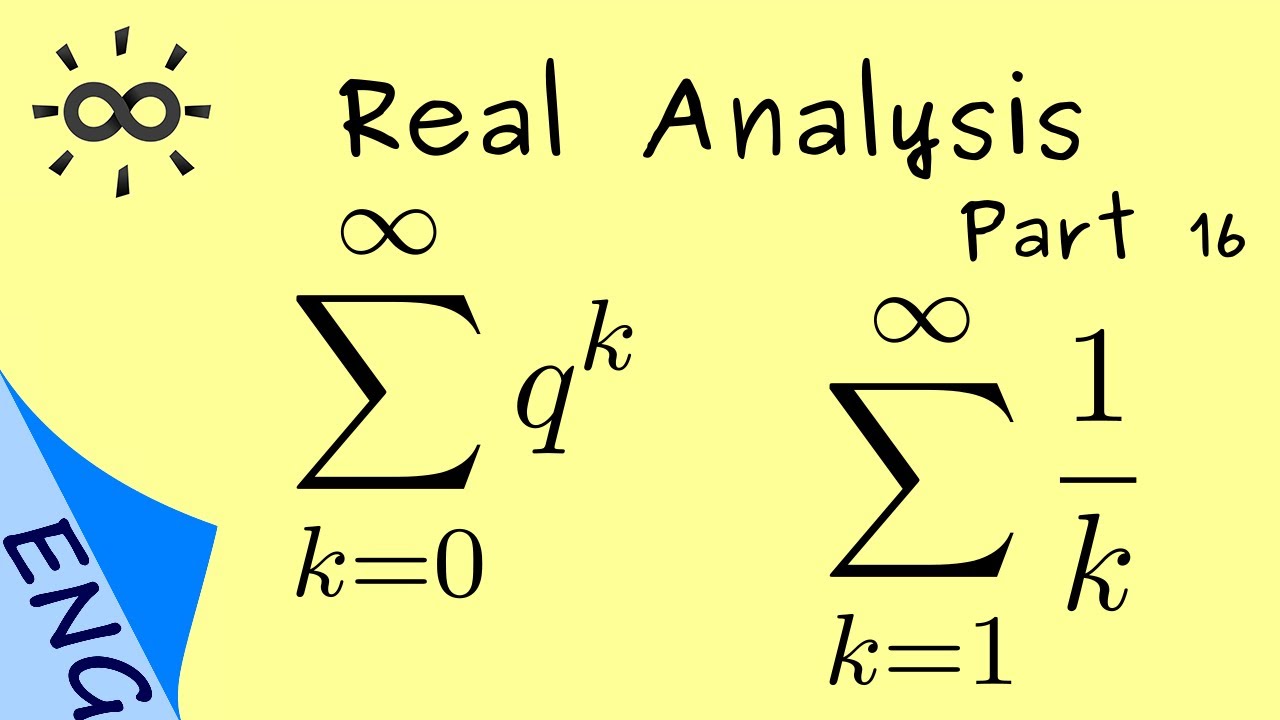Geometric and Harmonic Series
The most important examples of series.
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Series and Partial Sums | A series is a sequence of partial sums. |
Show consequences
| Concept | Content |
|---|---|
| Absolute Convergence | A strong concept of convergence of series. |
| Root Criterion | An important criterion to prove absolute convergence by means of the behavior of the n-th roots of the underlying sequence's terms. |
| Comparison Test | If a series converges can be checked with different tests. |
| Quotient Criterion | An important criterion to prove absolute convergence by means of ratios of the underlying sequence's terms. |
Study Geometric and Harmonic Series #
Before we give some criteria for the convergence of series, we first present the probably most important series and analyze their convergence.
Example 1.
For \(q\in\mathbb{K}\), the geometric series \[\sum_{k=0}^\infty q^k\] is convergent if and only if \(|q|<1\).
Proof: We can show that the \(n\)-th partial sum is given by \[s_n=\sum_{k=0}^nq^k=\begin{cases}\frac{1-q^{n+1}}{1-q}&:\text{ if }q\neq1,\\n+1&:\text{ if }q=1.\end{cases}\] Hence, \((s_n)_{n\in\mathbb{N}}\) is convergent if and only if \(|q|<1\). In this case we have \[\sum_{k=0}^\infty q^k=\lim_{n\to\infty}s_n=\lim_{n\to\infty}\frac{1-q^{n+1}}{1-q}=\frac{1}{1-q}.\]
The harmonic series \[\sum_{k=1}^\infty \frac1k\] is divergent to \(+\infty\).
Proof: If we construct some unbounded subsequence \((s_{n_l})_{l\in\mathbb{N}}\), the divergence of the harmonic series is proven (since it is monotonically increasing). Indeed, we now show the unboundedness of the subsequence \((s_{2^l})_{l\in\mathbb{N}}\): First, observe that \[s_{2^l}=s_1+(s_2-s_1)+(s_4-s_2)+(s_8-s_4)+\ldots+(s_{2^l}-s_{2^{l-1}})=s_1+\sum_{j=1}^l(s_{2^j}-s_{2^{j-1}}).\] Now we take a closer look to the number \(s_{2^j}-s_{2^{j-1}}\): By definition of \(s_n\), we have \[s_{2^j}-s_{2^{j-1}}=\sum_{k=2^{j-1}+1}^{2^j}\frac1k>\sum_{k=2^{j-1}+1}^{2^j}\frac1{2^{j}}= 2^{j-1}\frac1{2^{j}}=\frac12.\] The inequality in the above formula holds true since every summand is replaced by the smallest summand \(\frac1{2^{j}}\). The second last equality sign then comes from the fact that the number \(\frac1{2^{j}}\) is summed up \(2^{j-1}\)-times. Now using this inequality together with the above sum representation for \(s_{2^l}\), we obtain \[s_{2^l}=s_1+\sum_{j=1}^l(s_{2^j}-s_{2^{j-1}})>1+\sum_{j=1}^l\frac12=1+\frac{l}2.\] As a consequence, the subsequence \((s_{2^l})_{l\in\mathbb{N}}\) is unbounded.\(\Box\)For \(\alpha>1\), the sequence \[\sum_{k=1}^\infty \frac1{k^\alpha}\] is convergent.
Proof: The sequence of partial sums is strictly monotonically increasing due to \[s_{n+1}-s_n=\frac1{(n+1)^\alpha}\geq0.\] Therefore, by theorems about convergence of sequences, the convergence of \((s_n)_{n\in\mathbb{N}}\) is shown if we find some bounded subsequence \((s_{n_j})_{j\in\mathbb{N}}\). Again we use the representation for \(s_{2^j}-s_{2^{j-1}}\) as in example b). We can estimate \[\begin{aligned} s_{2^j}-s_{2^{j-1}}=&\,\sum_{k=2^{j-1}+1}^{2^j}\frac1{k^\alpha}<\sum_{k=2^{j-1}+1}^{2^j}\frac1{(2^{j-1}+1)^\alpha}\\ =&\,\frac{2^{j-1}}{(2^{j-1}+1)^\alpha}< \frac{2^{j-1}}{(2^{j-1})^\alpha}=\left(\frac{2}{2^\alpha}\right)^{j-1}=\left(\frac{1}{2^{\alpha-1}}\right)^{j-1}, \end{aligned}\] so we have \(s_{2^j}-s_{2^{j-1}}<q^{j-1}\) for \(q=\frac{1}{2^{\alpha-1}}\) and, due to \(\alpha>1\), it holds that \(0<q<1\). Using that \(s_1=1=q^0\), we obtain \[s_{2^l}=s_1+\sum_{j=1}^l(s_{2^j}-s_{2^{j-1}})<1+\sum_{j=0}^{l-1}q^j=1+\frac{1-q^l}{1-q}<1+\frac{1}{1-q}.\] Hence, the sequence \((s_{2^l})_{l\in\mathbb{N}}\) is bounded. This implies the desired result.\(\Box\)
Remark 2. Except for the first example, we have not
computed the limits of the other stated convergent series. We only
proved existence or non-existence of limits. Indeed, the computation of
limits of series is, in general, a very difficult issue and is not
possible in many cases.
The function \[\zeta(\alpha)=\sum_{k=1}^\infty
\frac1{k^\alpha}\] is very popular in analytic number theory
under the name Riemann Zeta Function. In b) and c), we have
implicitly proven that \(\zeta(\cdot)\)
is defined on the interval \((1,\infty)\) and has a pole at 1. This
function is subject of the Riemann hypothesis
which is one of the most important unsolved problems in modern
mathematics. Some known values of the Zeta function are (without proof)
\[\sum_{k=1}^\infty
\frac1{k^2}=\zeta(2)=\frac{\pi^2}6,\qquad
\sum_{k=1}^\infty \frac1{k^4}=\zeta(4)=\frac{\pi^4}{90},\qquad
\sum_{k=1}^\infty \frac1{k^6}=\zeta(6)=\frac{\pi^6}{945}.\]
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.