Limits of Functions
How function evaluations change when the argument approaches a certain point.
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Sequences | These object are needed to define limits later on. |
| Convergence | Convergent sequences have a well-defined limit. |
| Limit Theorems | Combining limits is a useful tool to deduce convergence and the limit of a more complicated sequence from the convergence of simpler building blocks. |
Show consequences
| Concept | Content |
|---|---|
| Continuity | The concept that relates functions with convergent sequences. |
| Theorem of l'Hospital | An important tool for calculating limits. |
| Improper Riemann Integrals | How to integrate on unbounded domains. |
Study Limits of Functions #
Now we begin to introduce the concept of continuity.
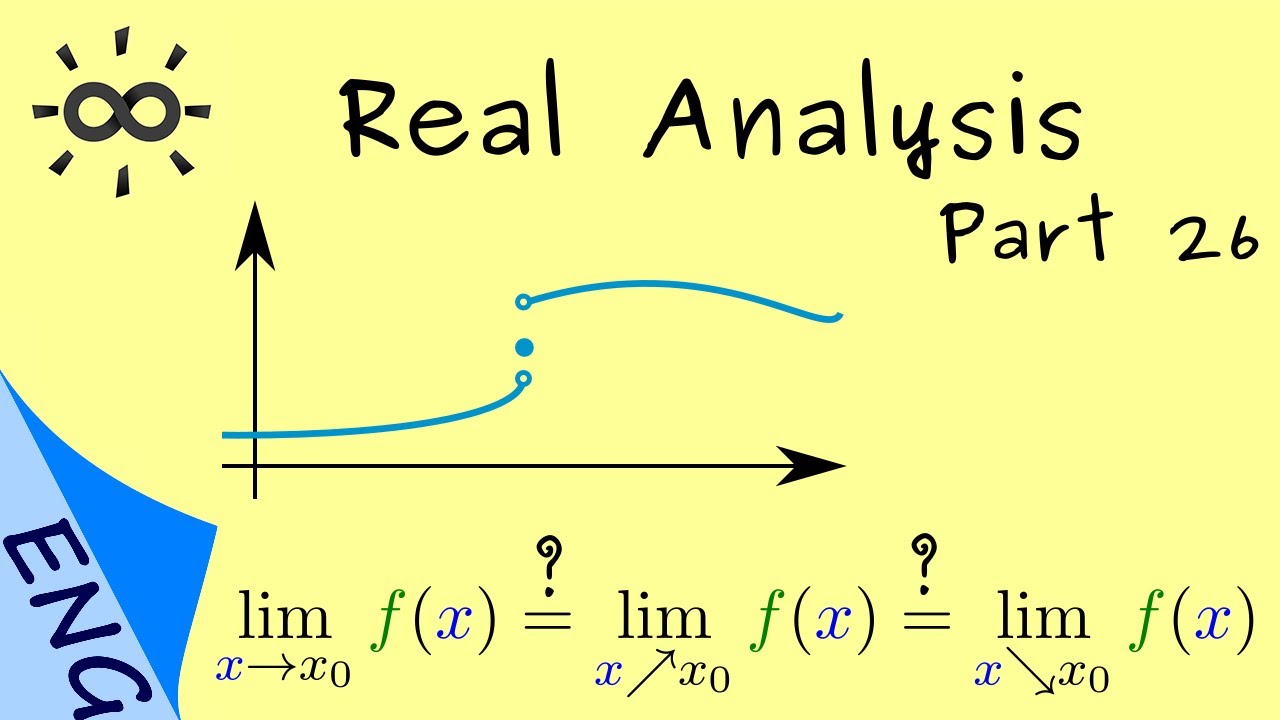
Definition 1 ((One-sided) limits of Functions). Let \(I\subset\mathbb{K}\), let \(f:I\to\mathbb{K}\) be a function, and let \(x_0\in I\). Then we define
the limit of \(f\) as \(x\) tends to \(x_0\) by \(c\in\mathbb{K}\) if for all sequences \((x_n)_{n\in\mathbb{N}}\) in \(I\backslash\{x_0\}\) with \(\lim_{n\to\infty}x_n=x_0\) holds \(\lim_{n\to\infty}f(x_n)=c\). In this case, we write \[\lim_{x\to x_0}f(x)=c\]
the limit of \(f\) as \(x\) tends from the left to \(x_0\) by \(c\in\mathbb{K}\) if \(I\subset \mathbb{R}\) and if for all sequences \((x_n)_{n\in\mathbb{N}}\) in \(\{x\in I\,:\,x< x_0\}\) with \(\lim_{n\to\infty}x_n=x_0\) holds \(\lim_{n\to\infty}f(x_n)=c\). In this case, we write \[\lim_{x\nearrow x_0}f(x)=c.\]
the limit of \(f\) as \(x\) tends from the right to \(x_0\) by \(c\in\mathbb{K}\) if \(I\subset \mathbb{R}\) and if for all sequences \((x_n)_{n\in\mathbb{N}}\) in \(\{x\in I\,:\,x>x_0\}\) with \(\lim_{n\to\infty}x_n=x_0\) holds \(\lim_{n\to\infty}f(x_n)=c\). In this case, we write \[\lim_{x\searrow x_0}f(x)=c.\]
In all three cases we assume that at least one sequence \((x_n)_{n\in\mathbb{N}}\) with the stated property exists.
Remark 2. From the above definition, we can also conclude that \(\lim_{x\to x_0}f(x)\) exists in the case \(I\subset \mathbb{R}\) if and only if \(\lim_{x\nearrow x_0}f(x)\) and \(\lim_{x\searrow x_0}f(x)\) exist and are equal. In this case, there holds \[\lim_{x\nearrow x_0}f(x)=\lim_{x\searrow x_0}f(x)=\lim_{x\to x_0}f(x).\] Though not explicitly introduced in the above definition, it should be intuitively clear what is meant by the following expressions \[\lim_{x\to\infty}f(x)=y,\qquad \lim_{x\to-\infty}f(x)=y,\qquad \lim_{x\to x_0}f(x)=\infty,\qquad \lim_{x\to x_0}f(x)=-\infty.\]
Example 3.
Consider the Heaviside function \(H:\mathbb{R}\to\mathbb{R}\) with \[H(x)=\begin{cases}1&,\text{ if }x\geq 0,\\0&,\text{ if }x<0.\end{cases}\] Then we have \(\lim_{x\nearrow 0}H(x)=0\), since for all \(x_n\in\mathbb{R}\) with \(x_n<0\) holds \(H(x_n)=0\). Further, \(\lim_{x\searrow 0}H(x)=1\), since for all \(x_n\in\mathbb{R}\) with \(x_n>0\) holds \(H(x_n)=1\). The limit \(\lim_{x\to 0}H(x)\) does not exist. E.g., take the sequence \(x_n=\frac{(-1)^n}n\). Then \[H(x_n)=\begin{cases}1:&\text{if $n$ is even,}\\0:&\text{if $n$ is odd.}\end{cases}\] Hence, \((H(x_n))_{n\in\mathbb{N}}\) is divergent.
Consider the function \(f:\mathbb{R}\to\mathbb{R}\) with \[f(x)=\begin{cases}1&,\text{ if }x= 0,\\0&,\text{ if }x\neq0.\end{cases}\] Then for all sequences \((x_n)_{n\in\mathbb{N}}\) in \(\mathbb{R}\backslash\{0\}\) holds that \((f(x_n))_{n\in\mathbb{N}}\) is a constant zero sequence. Hence, \(\lim_{x\to 0}f(x)=0\).
Consider a polynomial \(p:\mathbb{R}\to\mathbb{R}\) with \(p(x)=a_nx^n+\ldots+a_1x+a_0\) for some given \(a_0,\ldots,a_n\in\mathbb{R}\). Let \(x_0\in\mathbb{R}\). By the theorem on the calculation rules for limits of sequences of real numbers, we have that for all real sequences \((x_n)_{n\in\mathbb{N}}\) converging to \(x_0\) holds that \(p(x_n)\) converges to \(p(x_0)\), i.e., \[\lim_{x\to x_0}p(x)=p(x_0).\]
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.