A notion of integral for a simple class of functions.
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
Show consequences
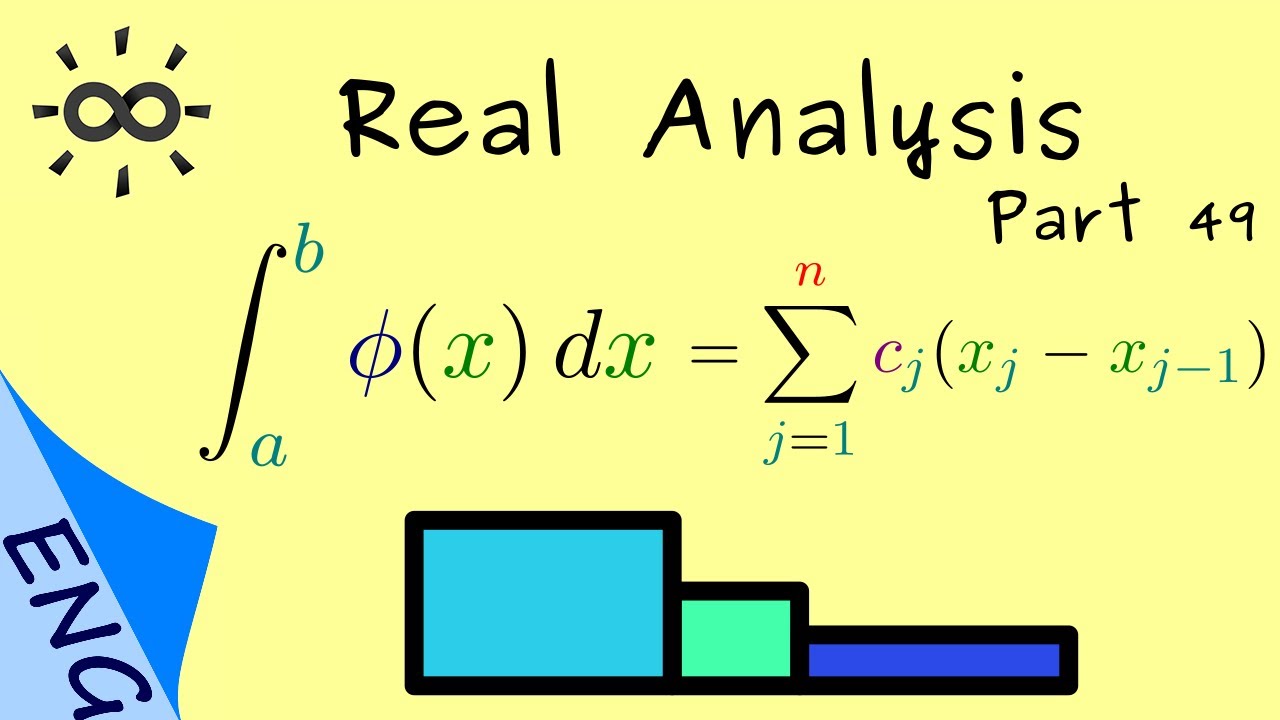
Definition 1 (Integral of step functions). Let
\(\phi\in\mathcal{T}([a,b])\) and
a decomposition \(\{x_0,\ldots,x_n\}\)
of \([a,b]\) be given such that for all
\(i=1,\ldots,n\) \[\phi(x)=c_i\text{ for all }x\in (x_{i-1},x_i)
.\] Then the integral of \(\phi\) is defined as \[\int_a^b\phi(x) \,
dx:=\sum_{j=1}^{n}c_j(x_{j}-x_{j-1}).\]
However, to be sure that the integral is well-defined we need
additionally that it is independent of the special choice of a
decomposition.
Lemma 2. \(\int_a^b\phi(x)\, dx\) is independent of
the choice of the decomposition, i.e., \(\int_a^b\phi(x)\, dx\) is well-defined for
all \(\phi\in\mathcal{T}([a,b])\).
Proof: Let \[\begin{aligned}
Z_1:\quad&a=x_0<x_1<x_2<\ldots<x_{n-1}<x_n=b,\\
Z_2:\quad&a=y_0<y_1<y_2<\ldots<y_{m-1}<y_m=b
\end{aligned}\] be two decompositions of \([a,b]\) such that \(\phi\) is constant on \((x_{i-1},x_i)\) and \(\phi\) is constant on \((y_{j-1},y_j)\) for all \(i=1,\ldots,n\), \(j=1,\ldots,m\). We distinguish between two
cases:
1st Case: \(Z_2\) is a refinement of \(Z_1\). This means that for all \(i\in\{1,\ldots,n\}\) there exists some
\(j(i)\in\{1,\ldots,m\}\) with \(x_i=y_{j(i)}\). Then for \(i\) holds \[x_i=y_{j(i)}<y_{j(i)+1}<\ldots<y_{j(i+1)}=x_{i+1}\]
and \(\phi(x)=d_k=c_i\) for \(x\in~(y_{k-1},y_k)\), \(k\in\{j(i-1)+1,\ldots,j(i)\}\). This
implies \[\begin{aligned}
\sum_{j=1}^{m}d_j(y_{j}-y_{j-1})=&\sum_{i=1}^{n}\sum_{k=j(i-1)+1}^{j(i)}c_i(y_{k}-y_{k-1})\\
=&\sum_{i=1}^{n}c_i\sum_{k=j(i-1)+1}^{j(i)}(y_{k}-y_{k-1})\\
=&\sum_{i=1}^{n}c_i(y_{j(i)}-y_{j(i-1)})=\sum_{i=1}^{n}c_i(x_i-x_{i-1}).
\end{aligned}\]
2nd Case: There exists a common
refinement \(Z_3\) of \(Z_1\) and \(Z_2\), i.e., \(Z_3=Z_1\cup Z_2\). Then we have (by using
the 1st case) \[\sum_{Z_1}...\;=\sum_{Z_3}\ldots\;=\sum_{Z_2}\ldots\;.\]
\(\Box\)
Discuss your questions by typing below.