Chain Rule
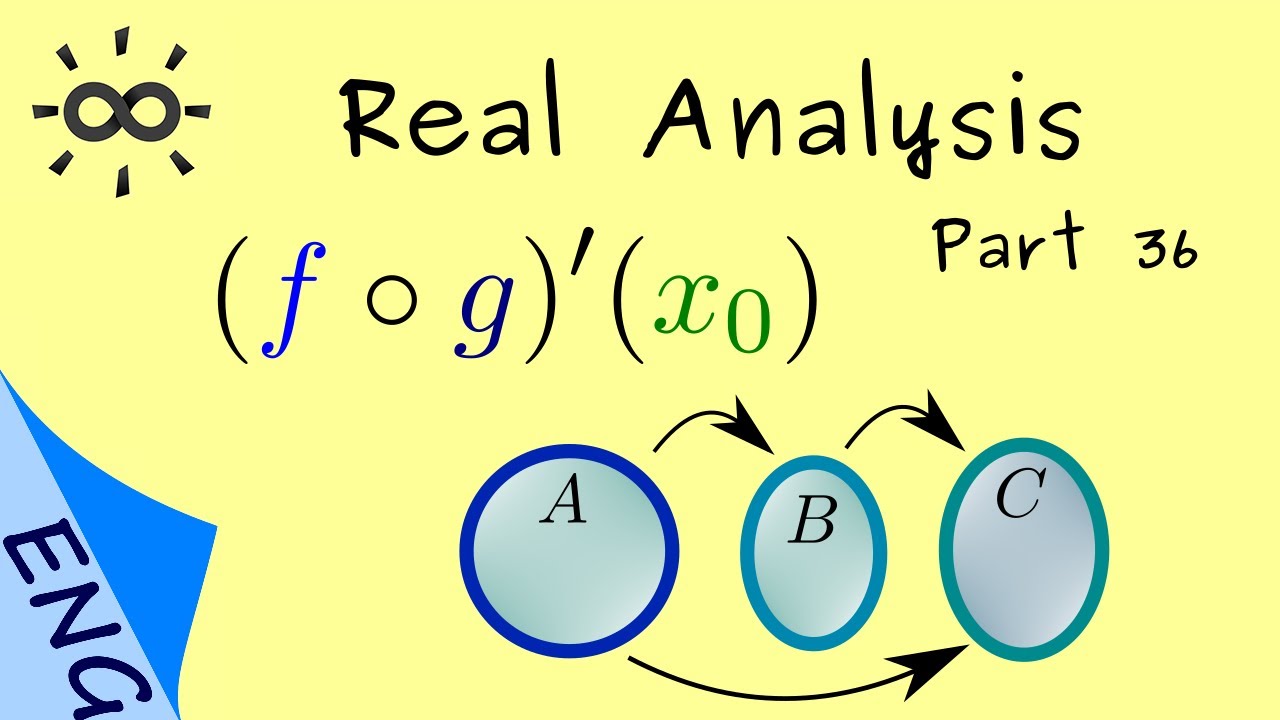
How to differentiate compositions of functions.
Discover Bridges
Study Chain Rule
Theorem 1 (Chain rule). Let \(I,J\) be intervals and \(f:J\to \mathbb{R}\) and \(g:I\to J\) be given. Assume that for \(x_0\in I\), \(g\) is differentiable in \(x_0\) and \(f\) is differentiable in \(g(x_0)\). Then the composition \(f\circ g\) (\((f\circ g)(x_0)=f(g(x_0))\)) is differentiable in \(x_0\) with \[(f\circ g)'(x_0)=f'(g(x_0))\cdot g'(x_0).\]
Proof: By assumption there are functions \(\Delta_{g,x_0}(x):I\rightarrow \mathbb{R}\) and \(\Delta_{f,g(x_0)}(y):J\rightarrow \mathbb{R}\) which are continuous in \(x_0\) and \(g(x_0)\) respectively such that \[\begin{aligned} g(x) &=& g(x_0)+(x-x_0)\Delta_{g,x_0}(x) \\ f(y) &=& f(g(x_0))+(y-g(x_0))\Delta_{f,g(x_0)}(y) \end{aligned}\] for all \(x\in I\) and \(y\in J\). Thus \[\begin{aligned} (f\circ g)(x) &=& f(g(x)) = f(g(x_0))+(g(x)-g(x_0))\Delta_{f,g(x_0)}(g(x)) \\ &=& f(g(x_0))+(x-x_0)\Delta_{g,x_0}(x)\Delta_{f,g(x_0)}(g(x_0)+(x-x_0)\Delta_{g,x_0}(x)) \end{aligned}\] for all \(x\in I\). Hence the function \[\begin{aligned} \Delta_{f\circ g}(x) &:=& \Delta_{g,x_0}(x)\Delta_{f,g(x_0)}(g(x_0)+(x-x_0)\Delta_{g,x_0}(x)) \end{aligned}\] fulfills \[\begin{aligned} (f\circ g)(x) &=& (f\circ g)(x_0))+(x-x_0)\Delta_{f\circ g}(x) \end{aligned}\] for all \(x\in I\). As a composition of functions that are continuous in \(x_0\) it is also continuous in \(x_0\) with \(\Delta_{f\circ g}(x_0)= \Delta_{g,x_0}(x_0)\Delta_{f,g(x_0)}(g(x_0)) =g'(x_0)f'(g(x_0))\). \(\Box\)
Example 2.
\(f:\mathbb{R}\to\mathbb{R}\) with \(f(x)=\sin(x^2)\), then \(f'(x)=\cos(x^2)\cdot 2x\).
Let \(a\in\mathbb{R}\). Consider \(f:\mathbb{R}\to\mathbb{R}\) with \(f(x)=a^x=\exp(x\log(a))\), then \[f'(x)=\exp(x\log(a))\cdot\log(a)=a^x\cdot\log(a).\]
Let \(a\in\mathbb{R}\). Consider \(f:\mathbb{R}^+\to\mathbb{R}\) with \(f(x)=x^a=\exp(a\log(x))\), then \[f'(x)=\exp(a\log(x))\cdot\frac{a}x=x^a\cdot \frac{a}x=a\cdot x^{a-1}.\]
Consider \(f:\mathbb{R}^+\to\mathbb{R}\) with \(f(x)=x^x=\exp(x\log(x))\), then \[f'(x)=\exp(x\log(x))\cdot\left(\frac{x}x+\log(x)\right)=x^x\cdot (1+\log(x)).\]
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.