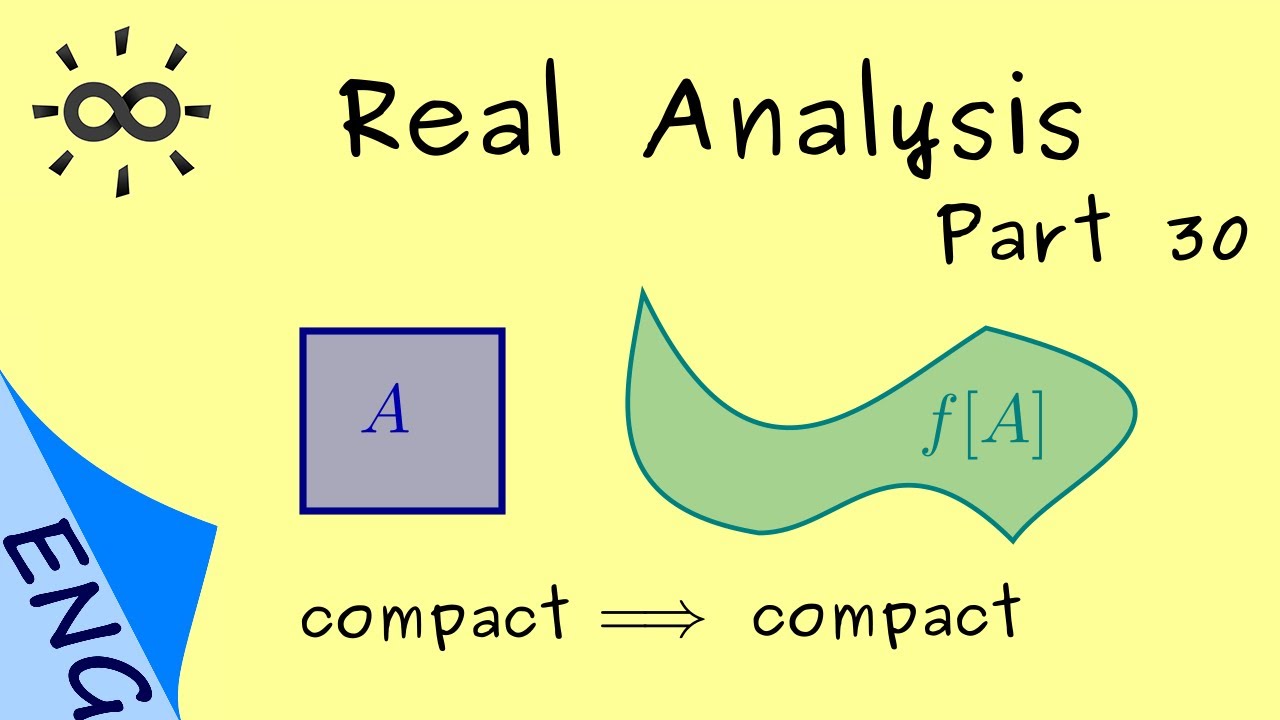
A mapping property for continuous functions.
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
Show consequences
| Concept |
Content |
| Rolle's Theorem |
The derivatives of functions with equal boundary conditions always have at least one zero. |
Theorem 1 (Continuous functions defined on a compact
set). Let \(I\subset\mathbb{K}\) be
compact and let \(f:I\to\mathbb{K}\) be
continuous. Then \(f(I)\) is compact.
In particular, by the Theorem of Heine-Borel, \(f(I)\) is bounded and closed. If further
\(f(I) \subset \mathbb{R}\), so that
there exist \(x^+,x^-\in I\) such that
\[f(x^+)=\max\{f(x)\,:\,x\in I\},\qquad
f(x^-)=\min\{f(x)\,:\,x\in I\}.\]
Proof. Let \((y_n)_{n\in\mathbb{N}}\) be a sequence in
\(f(I)\). Then for each \(n\in\mathbb{N}\) there is an \(x_n\in I\) such that \(y_n=f(x_n)\). Since \(I\) is compact, there exists a subsequence
\((x_{n_k})_{k\in\mathbb{N}}\) that
converges to some \(x\in I\). Now,
since \(f\) is continuous, we have
\[\lim_{k\rightarrow \infty} y_{n_k} =
\lim_{k\rightarrow \infty} f(x_{n_k}) = f(x)=:y \in f(I).\] Hence
we found a subsequence \((y_{n_k})_{k\in\mathbb{N}}\) of \((y_n)_{n\in\mathbb{N}}\) that converges in
\(f(I)\). Therefore \(f(I)\) is compact. ◻
Fabian Gabel and Marcus Waurick. Well-defined & Wonderful podcast, marcus-waurick.de.
Discuss your questions by typing below.