Composition
The composition for maps is just applying two maps in a row.
Discover Bridges
Study Composition
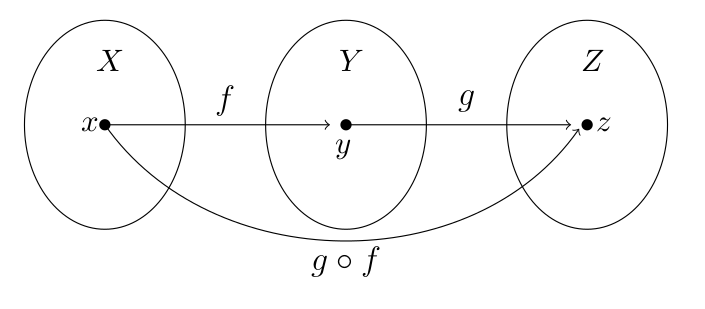
Definition 1. If \(f:X \to Y\) and \(g : Y\to Z\), we may compose, or concatenate these maps: \[\begin{aligned} g \circ f : X &\to Z\\ x &\mapsto g(f(x)) \end{aligned}\] We call \(g \circ f\) the composition of the two functions.
Usually, \(g\circ f \neq f\circ g\), the latter does not even make sense, in general. \[X \to Y \to Z\]
Example 2.
\(f: \mathbb{R} \rightarrow \mathbb{R}\), \(x\mapsto x^2\); \(g:\mathbb{R} \rightarrow \mathbb{R}\), \(x\mapsto \sin(x)\) \[\begin{aligned} g\circ f: \mathbb{R} &\rightarrow \mathbb{R} \\ x &\mapsto \sin(x^2) \\ f\circ g: \mathbb{R} &\rightarrow \mathbb{R} \\ x &\mapsto (\sin(x))^2 \end{aligned}\]
Let \(X\) be a set. Then \(\operatorname{id}_X: X\rightarrow X\) with \(x\mapsto x\) is called the identity map. If there is no confusion, one usually writes \(\operatorname{id}\) instead of \(\operatorname{id}_X\). Let \(f: X\rightarrow X\) be a function. Then \[f\circ \operatorname{id}=f=\operatorname{id}\circ f.\]
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.