Uniform Convergence
A strong notion of convergence for sequences of functions that helps to preserve favorable properties like continuity in the limit.
On this page
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Pointwise Convergence | A notion of convergence for sequences functions that reduces the question of convergence to convergence of sequences of real numbers. |
| Sequences of Bounded Functions | The concept of sequences but for functions instead of real numbers. |
Show consequences
| Concept | Content |
|---|---|
| Uniform Limits of Continuous Functions | How to preserve continuity in the limit of a sequence of continuous functions. |
| Uniform Convergence for Differentiable Functions | Compatibility of differentiability with uniform limits. |
Study Uniform Convergence #
We now present an alternative convergence concept for functions:
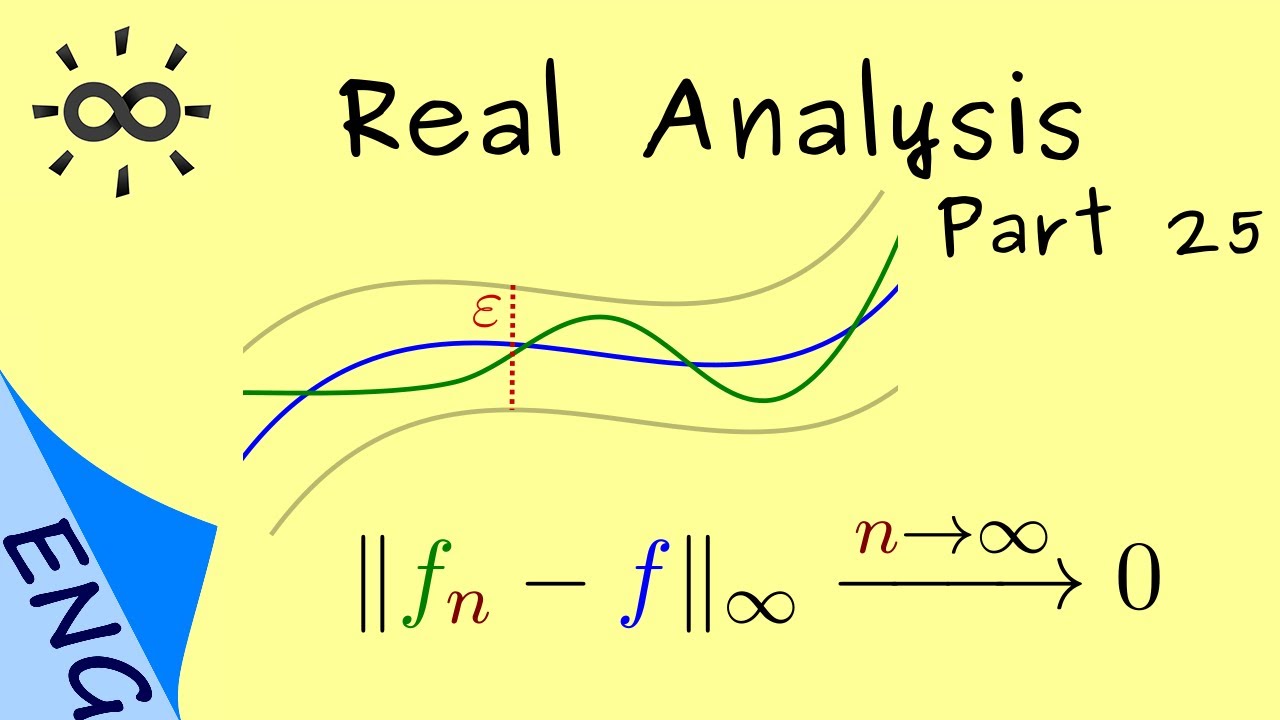
Definition 1 (Uniform convergence). A sequence \((f_n)_{n\in\mathbb{N}}\) of functions \(f_n:I\to\mathbb{K}\) is called uniformly convergent to \(f:I\to\mathbb{K}\) if for all \(\varepsilon>0\) there exists some \(N\) such that for all \(n\geq N\) and \(x\in I\) holds \[|f(x)-f_n(x)|<\varepsilon.\] Using logical quantifiers this reads (compare with the quantifiers for pointwise convergence!): \[\label{def:lunifconv} \forall \varepsilon > 0 \quad \exists N \in \mathbb{N} \quad \forall n \geq N \quad \forall x \in I \quad : \quad |f_n(x)-f(x)|<\varepsilon \ .\]
As a rule of thumb, you can think of pushing one quantifier to the right but, of course, this will change a lot. The interpretation is that we can measure the distance between two functions \(f\) und \(g\) as the largest distance between the two graphs, that means the distance you can measure at a given point: \[\sup_{x \in I} | f(x) - g(x) |\] We have the uniform convergence if this measured distance between \(f_n\) and \(f\) is convergent to zero. (See below.)
We will now see that uniform convergence is a stronger property than pointwise convergence.
Theorem 2 (Uniform convergence implies pointwise convergence). Let a sequence \((f_n)_{n\in\mathbb{N}}\) with \(f_n:I\to\mathbb{K}\) be uniformly convergent to \(f:I\to\mathbb{K}\). Then \((f_n)_{n\in\mathbb{N}}\) is also pointwisely convergent to \(f\).
Proof: Let \(\varepsilon>0\). Then there exists some \(N\) such that for all \(n\geq N\) and \(x\in I\) holds \[|f(x)-f_n(x)|<\varepsilon.\] In particular, for some arbitrary \(x\in I\) holds \[|f(x)-f_n(x)| <\varepsilon.\] Hence, the sequence \((f_n(x))_{n\in\mathbb{N}}\) in \(\mathbb{K}\) converges to \(f(x)\).\(\Box\)
Remark 3. Uniform convergence to \(f:I\to\mathbb{K}\) means that for all \(\varepsilon>0\) holds that all (except finitely many) functions \(f_n\) are “inside some \(\varepsilon\)-stripe around \(f\)”.
Theorem 4. A sequence \((f_n)_{n\in\mathbb{N}}\) of functions \(f_n:I\to\mathbb{K}\) converges uniformly to \(f:I\to\mathbb{K}\), if, and only if, \[\lim_{n\to\infty}||f_n-f||_\infty=\lim_{n\to\infty}\sup\{|f(x)-f_n(x)|\;:\;x\in I\}=0.\] This means that uniform convergence is nothing but convergence with respect to the infinity norm \(||\cdot||_\infty\) .
Proof. Assume that \((f_n)_{n\in\mathbb{N}}\) converges
uniformly to \(f\). Let \(\varepsilon>0\). Then there exists some
\(N\) such that for all \(n\geq N\) and \(x\in I\) holds \[|f(x)-f_n(x)|<\frac\varepsilon2.\]
Therefore, for all \(n\geq N\), we have
\[\sup\{|f(x)-f_n(x)|\;:\;x\in
I\}\leq\frac\varepsilon2<\varepsilon,\] and thus, the equation
in Theorem 4 holds true.
Conversely, assuming that the equation in Theorem 4 holds true, we obtain that for
\(\varepsilon>0\), there exists some
\(N\) with the property that for all
\(n\geq N\) holds \[\sup\{|f(x)-f_n(x)|\;:\;x\in
I\}<\varepsilon.\] This means that for all \(n\geq N\) and \(x\in I\), there holds that \[|f(x)-f_n(x)|<\varepsilon.\] However,
this statement is nothing but uniform convergence of \((f_n)_{n\in\mathbb{N}}\) towards \(f\). ◻
Example 5.
Let \(I=[0,1]\) and consider the sequence \(f_n(x)= x^n\). Then we have the pointwise limit \[f(x)=\lim_{n\to\infty}f_n(x)=\begin{cases}0&,\text{ if }x\in[0,1),\\1&,\text{ if }x=1.\end{cases}\] Is \((f_n)_{n\in\mathbb{N}}\) also uniformly convergent to \(f\)?
The answer is no, since for \(x_n=1/\sqrt[n]{2}\), there holds \[|f(x_n)-f_n(x_n)|=\left|0-{\textstyle\frac12}\right|={\textstyle\frac12}.\]We now consider the same sequence on the smaller interval \([0,\frac12]\). The pointwise limit is now \(f=0\). For \(n\in\mathbb{N}\), we have \[\sup\left\{|f(x)-f_n(x)|\,:\,x\in[0,{\textstyle\frac12}]\right\}=\sup\left\{x^{n}:\,x\in[0,{\textstyle\frac12}]\right\}=\frac1{2^n}.\]
Therefore \[\lim_{n\to\infty}\sup\left\{|f(x)-f_n(x)|\,:\,x\in[0,{\textstyle\frac12}]\right\}=0\] and hence, we have uniform convergence.
Define the function \(f_n:[0,1]\to\mathbb{R}\) by \[f_n(x)=\begin{cases}n^2x(1-nx)&,\text{ if }x\in[0,\frac1n[,\\0&,\text{ if }x\in[\frac1n,1].\end{cases}\]
Then for all \(x\in[0,1]\) holds \[\lim_{n\to\infty}f_n(x)=0\] since \(f_n(0)=0\) and \(f_n(x)=0\) if \(x>\frac1n\). The sequence \((f_n)_{n\in\mathbb{N}}\) is however not uniformly convergent to \(f=0\), since \[\sup\{|f_n(x)-0|\,:\,x\in[0,1]\}\geq\left|f_n\left({\textstyle\frac1{2n}}\right)\right|=\frac{n}4.\]
Theorem 6. Let \((f_n)_{n\in\mathbb{N}}\) be a sequence of bounded functions \(f_n:I\to\mathbb{K}\). Assume that \((f_n)_{n\in\mathbb{N}}\) converges uniformly to \(f:I\to\mathbb{K}\). Then \(f\) is bounded.
Proof: For \(\varepsilon=1\), there exists some \(N\) such that for all \(n\geq N\) and \(x\in I\) holds \[|f_n(x)-f(x)|<1.\] In particular, we have \(|f_N(x)-f(x)|<1\) for all \(x\in I\). This consequences that for all \(x\in I\), there holds \[|f(x)|<|f_N(x)|+1.\] The boundedness of \(f_N\) then implies the boundedness of \(f\). \(\Box\)
Remark 7. Note that the assumption of uniform
convergence is essential for the boundedness of \(f\). For instance, consider the sequence
\((f_n)_{n\in\mathbb{N}}\) of bounded
functions \(f_n:[0,\infty)\to\mathbb{R}\) with \[f_n(x)=\begin{cases}x:&\text{ if
}x<n\\0:&\text{ else.}\end{cases}\] First we argument that
\((f_n)_{n\in\mathbb{N}}\) converges
pointwisely to \(f:[0,\infty)\rightarrow
\mathbb{R}\) with \(f(x)=x\):
Let \(x \in[0,\infty)\). Then there
exists some \(N\in\mathbb{N}\) with
\(x<N\). Hence, for all \(n\geq N\), we have \(f_n(x)=x\). This implies convergence to
\(f:[0,\infty)\to\mathbb{R}\) with
\(f(x)=x\).
Second we state that each \(f_n\) is
bounded: This is a consequence of the fact that, by the definition of
\(f_n\), there holds \(f_n(x)<n\) for all \(x\in[0,\infty)\).
Altogether, we have found a sequence of bounded functions pointwisely
converging to some unbounded function. Hence, Theorem 6 is no longer valid, if we
replace the phrase “uniformly convergent” by “pointwisely
convergent”.
Discuss your questions by typing below.
Solve the Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.