Sequences of Bounded Functions

The concept of sequences but for functions instead of real numbers.

Discover Bridges

Click on an arrow to get a description of the connection!

Click on an arrow to get a description of the connection!

Show requirements
Concept Content
Bounded Sets, Maxima and Minima The values inside a set of real numbers can be bounded.
Supremum and Infimum of Sets Bounded sets always have an supremum and infimum which are generalizations of maximum and minimum.
Maps Maps are the mathematical formulation of a machine that gets inputs and generate outputs. On both sides, sets are needed for the domain and the codomain.
Image and Preimage Via images and preimages we describe how functions work on sets.
Sequences These object are needed to define limits later on.
Sets Sets are the basic building blocks for a lot of mathematics. In order to rigorously define numbers and doing real analysis, we need to know how to work with sets.
Show consequences
Concept Content
Pointwise Convergence A notion of convergence for sequences functions that reduces the question of convergence to convergence of sequences of real numbers.
Uniform Limits of Continuous Functions How to preserve continuity in the limit of a sequence of continuous functions.
Exponential Function A special function that can be defined via a power series.
Power Series A sequence of partial sums of polynomial functions.
Uniform Convergence A strong notion of convergence for sequences of functions that helps to preserve favorable properties like continuity in the limit.
Uniform Convergence for Differentiable Functions Compatibility of differentiability with uniform limits.

Study Sequences of Bounded Functions

Definition 1 (Bounded functions). Let \(I\) be a set. Then we call a function \(f:I\rightarrow \mathbb{K}\) bounded, if \[\sup\{|f(x)|\,:\,x\in I\}<\infty.\]

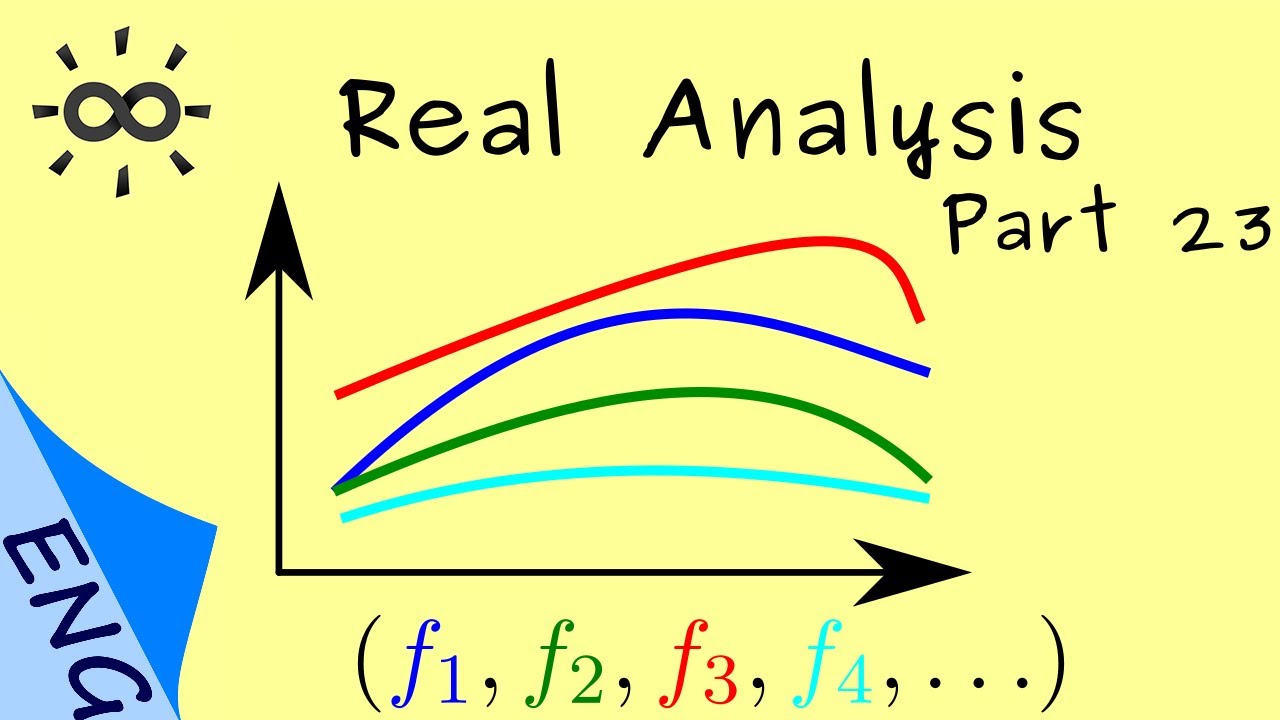
Definition 2 (Sequence of functions). Let \(I\) be a set and for all \(n \in \mathbb{N}\), let \(f_n :I\rightarrow \mathbb{K}\) be bounded. Then \((f_1, f_2, f_3, f_4, \dots)\) is a sequence of functions.

Not that, for any fixed point \(x \in I\), we get an ordinary sequence of real numbers \[\begin{aligned} (f_1(x), f_2(x), f_3(x), f_4(x), \dots). \end{aligned}\]

Open video on YouTube

Discuss your questions by typing below.

Solve the Exercise

The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.

← Sequences
Series and Partial Sums →