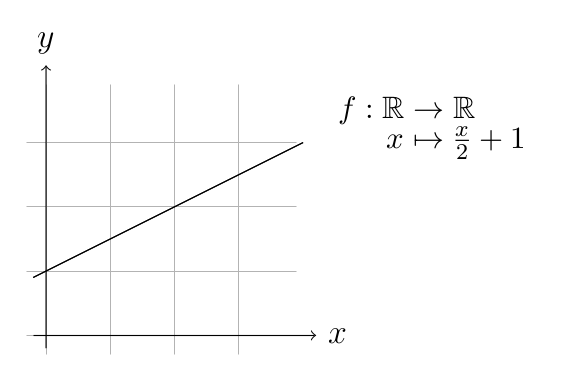Injectivity, Surjectivity, Bijectivity
These are important notions for maps.
Discover Bridges
Study Injectivity, Surjectivity, Bijectivity
Definition 1 (Injective, surjective and bijective). A map \(f: X \to Y\) is called
injective if every fiber of \(f\) has only one element: \(x_1 \neq x_2 \Rightarrow f(x_1) \neq f(x_2)\).
surjective if \(\mathrm{Ran}(f)=Y\). With quantifiers: \(\forall y\in Y~ \exists x\in X \,:\, f(x)=y\).
bijective if \(f\) is both injective and surjective.
Example 2. Define the function that maps each student to her or his chair. This means that \(X\) is the set of all students in the room, and \(Y\) the set of all chairs in the room.
well-defined: every student has a chair
surjective: every chair is taken
injective: on each chair there is no more than one student
bijective: every student has his/her own chair, and no chair is empty
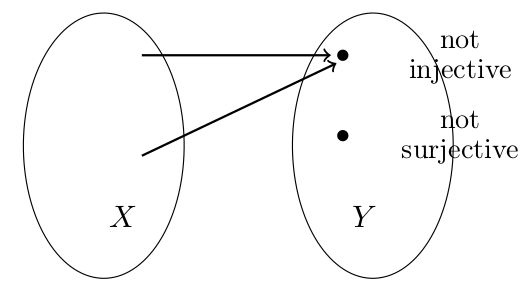
Rule of Thumb 3. Surjective, injective, bijective A map \(f: X \rightarrow Y\) is \[\begin{aligned} \text{surjective}\ &\Leftrightarrow\ \text{at each } y\in Y \text{ arrives at least one arrow} \\ &\Leftrightarrow\ f(X)=Y\\ &\Leftrightarrow\ \text{the equation } f(x)=y \text{ has for all } y\in Y \text{ a solution} \\ \\ \text{injective}\ &\Leftrightarrow\ \text{at each } y\in Y \text{ arrives at most one arrow}\\ &\Leftrightarrow\ \left( x_1 \neq x_2\quad \Rightarrow\quad f(x_1)\neq f(x_2) \right) \\ &\Leftrightarrow\ \left( f(x_1)=f(x_2)\quad \Rightarrow\quad x_1=x_2 \right) \\ &\Leftrightarrow\ \text{the equation } f(x)=y \text{ has for all } y\in f(X) \text{ a unique solution} \\ \\ \text{bijective}\ &\Leftrightarrow\ \text{at each } y\in Y \text{ arrives exactly one arrow} \\ &\Leftrightarrow\ \text{the equation } f(x)=y \text{ has for all } y\in Y \text{ a unique solution} \end{aligned}\]
Thus, if \(f\) is bijective, there is a well defined inverse map \[\begin{aligned} f^{-1}:Y&\to X\\ y &\mapsto x \text{ where } f(x)=y \,. \end{aligned}\] Then \(f\) is called invertible and \(f^{-1}\) is called the inverse map of \(f\).
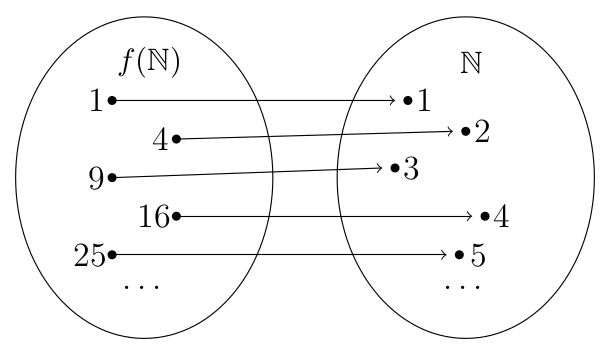
Example 4. Consider the function \(f: \mathbb{N} \rightarrow \{1, 4, 9, 16, \ldots\}\) given by \(f(n) = n^2\). This is a bijective function. The inverse map \(f^{-1}\) is given by: \[\begin{aligned} f^{-1}:\lbrace1,4,9,16,25,\dots \rbrace &\rightarrow \mathbb{N} \\ m & \mapsto \sqrt{m} \\ \text{or: } n^2 &\mapsto n \end{aligned}\]
Example 5. For a function \(f:\mathbb{R}\rightarrow\mathbb{R}\), we can sketch the graph \(\lbrace(x,f(x)): x\in X\rbrace\) in the \(x\)-\(y\)-plane:
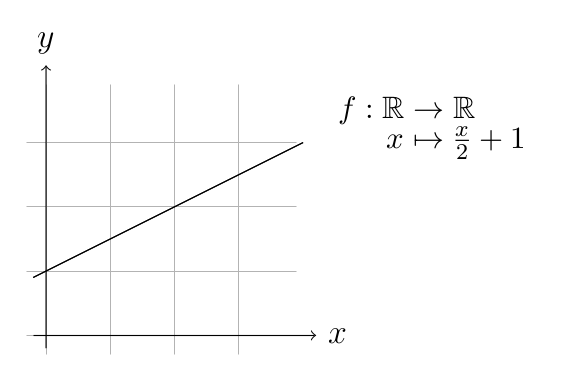
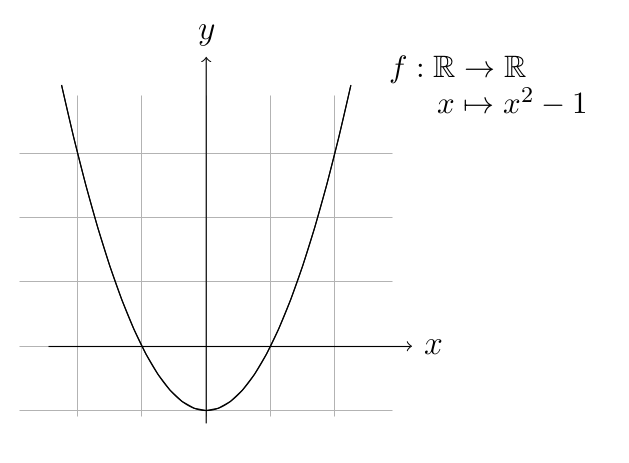
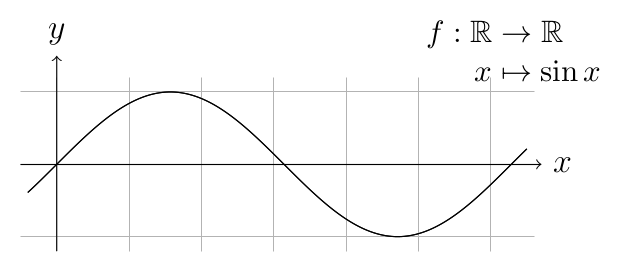
Which of the functions are injective, surjective or bijective?
These notions might seem a little bit off-putting, but we will use them so often that you need to get use to them. Maybe the video will help you as well.
Discuss your questions by typing below.
Solve the WeBWorK Exercise
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.