Continuity
The concept that relates functions with convergent sequences.
On this page
Discover Bridges #
Click on an arrow to get a description of the connection!
Click on an arrow to get a description of the connection!
Show requirements
| Concept | Content |
|---|---|
| Maps | Maps are the mathematical formulation of a machine that gets inputs and generate outputs. On both sides, sets are needed for the domain and the codomain. |
| Convergence | Convergent sequences have a well-defined limit. |
| Limits of Functions | How function evaluations change when the argument approaches a certain point. |
Show consequences
| Concept | Content |
|---|---|
| Logarithm Function | The inverse of the exponential function. |
| Differentiability | How to quantify the rate of change of a function. |
| Exponential Function | A special function that can be defined via a power series. |
| Continuity for Sums, Products, Quotients, and Compositions | How combination of continuous functions leads to new continuous functions. |
| Continuous Images of Compact Sets Are Compact | A mapping property for continuous functions. |
| Intermediate Value Theorem | This theorem tells us that continuous functions don't jump. They have to attain every value between two values in their image. |
| Uniform Limits of Continuous Functions | How to preserve continuity in the limit of a sequence of continuous functions. |
| Epsilon-Delta Definition | A different notion of continuity using open intervals. If the input to a continuous function varies less than delta, then the output values should vary less than epsilon. |
Study Continuity #
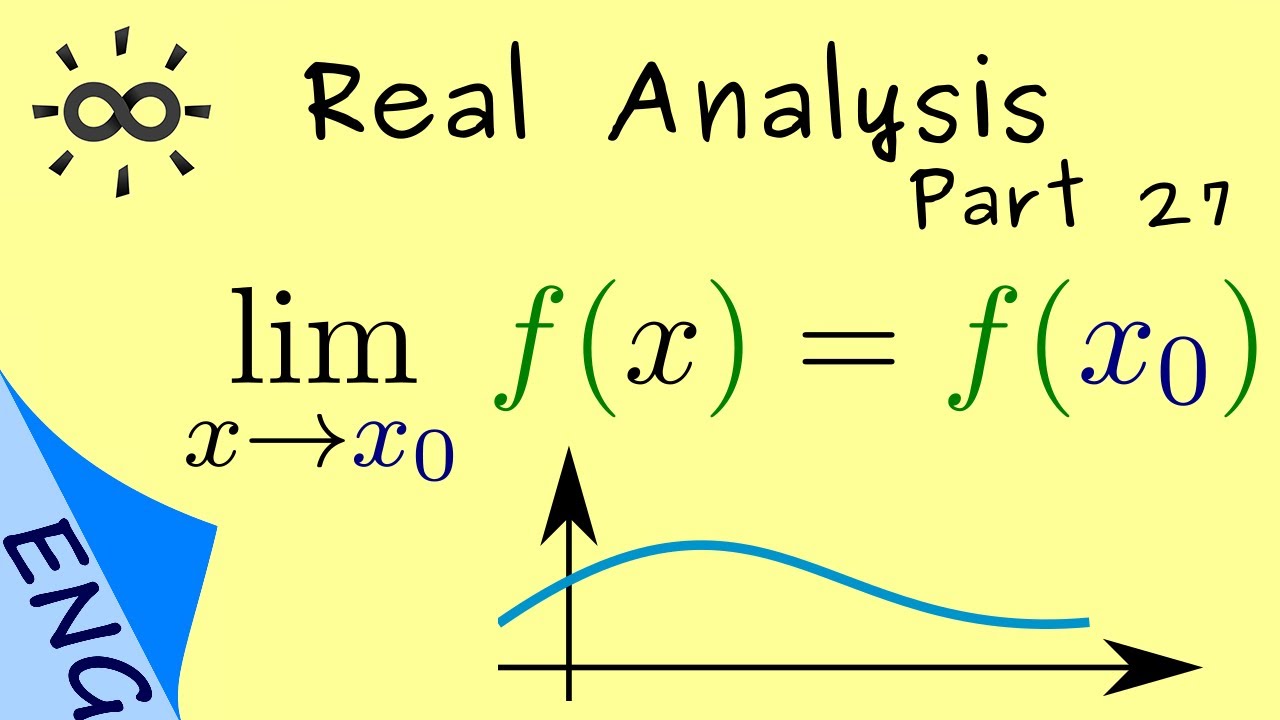
Definition 1 (Continuity). Let \(I\subset\mathbb{K}\) and let \(f:I\to\mathbb{K}\) be a function. Then \(f\) is called continuous in \(x_0\in I\) if \[\lim_{x\to x_0}f(x)=f(x_0).\] Moreover, \(f\) is called continuous on \(I\) if it is continuous in \(x_0\) for all \(x_0\in I\).
Remark 2. Sometimes we will just say \(f:I\to\mathbb{K}\) is continuous whereby we mean it is continuous on \(I\).
Example 3.
The constant function \(f:\mathbb{R}\to\mathbb{R}\) with \(f(x)=c\) for some \(c\in\mathbb{R}\) is continuous on \(\mathbb{R}\).
The Heaviside function \[H(x)=\begin{cases}1&,\text{ if }x\geq 0,\\0&,\text{ if }x<0.\end{cases}\] is discontinuous at \(x_0=0\), but continuous everywhere else.
The function \(f:\mathbb{R}\to\mathbb{R}\) \[f(x)=\begin{cases}1&,\text{ if }x= 0,\\0&,\text{ if }x\neq0.\end{cases}\] is discontinuous at \(x_0=0\), but continuous everywhere else.
Polynomials are continuous on \(\mathbb{R}\).
Rational functions \(f:I\to\mathbb{K}\) with \(f(x)=\frac{p(x)}{q(x)}\) for some polynomials \(p,q\) (\(q\) is not the zero polynomial) are defined on \(I=\{x\in\mathbb{R}\,:\,q(x)\neq0\}\) and are continuous on \(I\) (due to the formulae for convergent sequences).
The absolute value function \(|\cdot|:\mathbb{R}\to\mathbb{R}\), i.e., \[|x|=\begin{cases}x&,\text{ if }x\geq 0,\\-x&,\text{ if }x<0.\end{cases}\] is continuous on \(\mathbb{R}\).
The function \(f:\mathbb{R}\to\mathbb{R}\) with \[f(x)=\begin{cases}1&,\text{ if }x\in\mathbb{Q},\\0&,\text{ if }x\notin\mathbb{Q}\end{cases}\] is everywhere discontinuous.
Proof: Let \(x_0\in\mathbb{R}\):
First case: \(x_0\in\mathbb{Q}\). Then take a sequence \((x_n)_{n\in\mathbb{N}}\) with \(\lim_{n\to \infty}x_n=x_0\) and \(x_n\in\mathbb{R}\backslash\mathbb{Q}\) (for instance, \(x_n=x_0+\frac{\sqrt{2}}{n}\)). Then \(f(x_n)=0\) for all \(n\in\mathbb{N}\) and thus \(\lim_{n\to \infty}x_n=0\neq f(x_0)=1\).
Second case: \(x_0\in\mathbb{R}\backslash\mathbb{Q}\). Then take a sequence \((x_n)_{n\in\mathbb{N}}\) with \(\lim_{n\to \infty}x_n=x_0\) and \(x_n\in\mathbb{Q}\) (this exists since every real number can be approximated by a rational number in arbitrary good precision). Then \(f(x_n)=1\) for all \(n\in\mathbb{N}\) and thus \(\lim_{n\to \infty}x_n=1\neq f(x_0)=0\).
Discuss your questions by typing below.
Solve the WeBWorK Exercise #
The data for the interactive network on this webpage was generated with pntfx Copyright Fabian Gabel and Julian Großmann. pntfx is licensed under the MIT license. Visualization of the network uses the open-source graph theory library Cytoscape.js licensed under the MIT license.